I forgot one line when pasted the code in the forum  , here it is:
, here it is:
final RandomGenerator random = new Well19937c(0x9e9409e2520c1fc3l); // you can change this seed as you like, it's just a seed
Good.
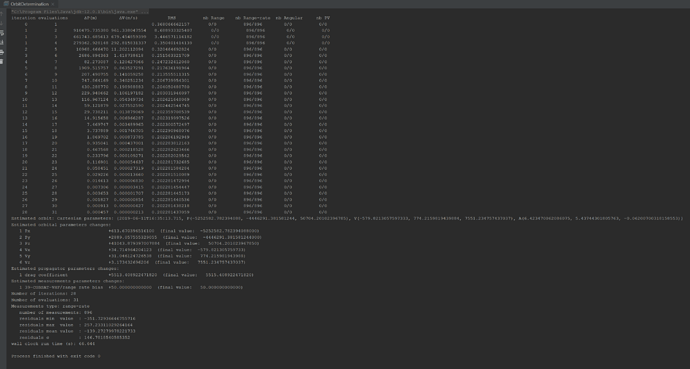
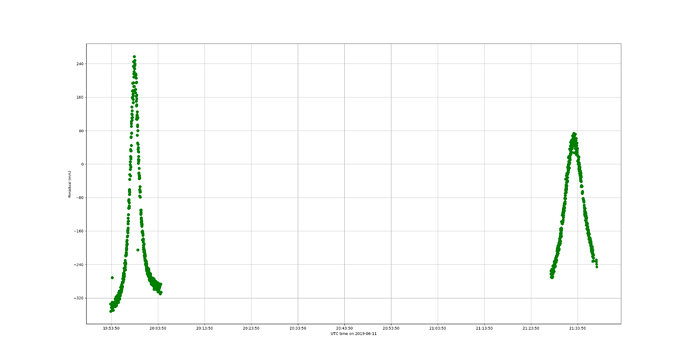
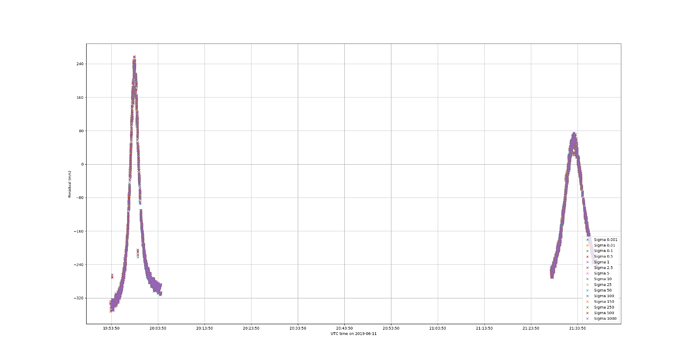
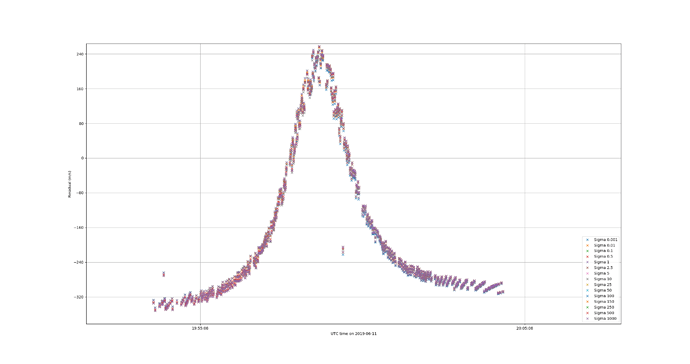
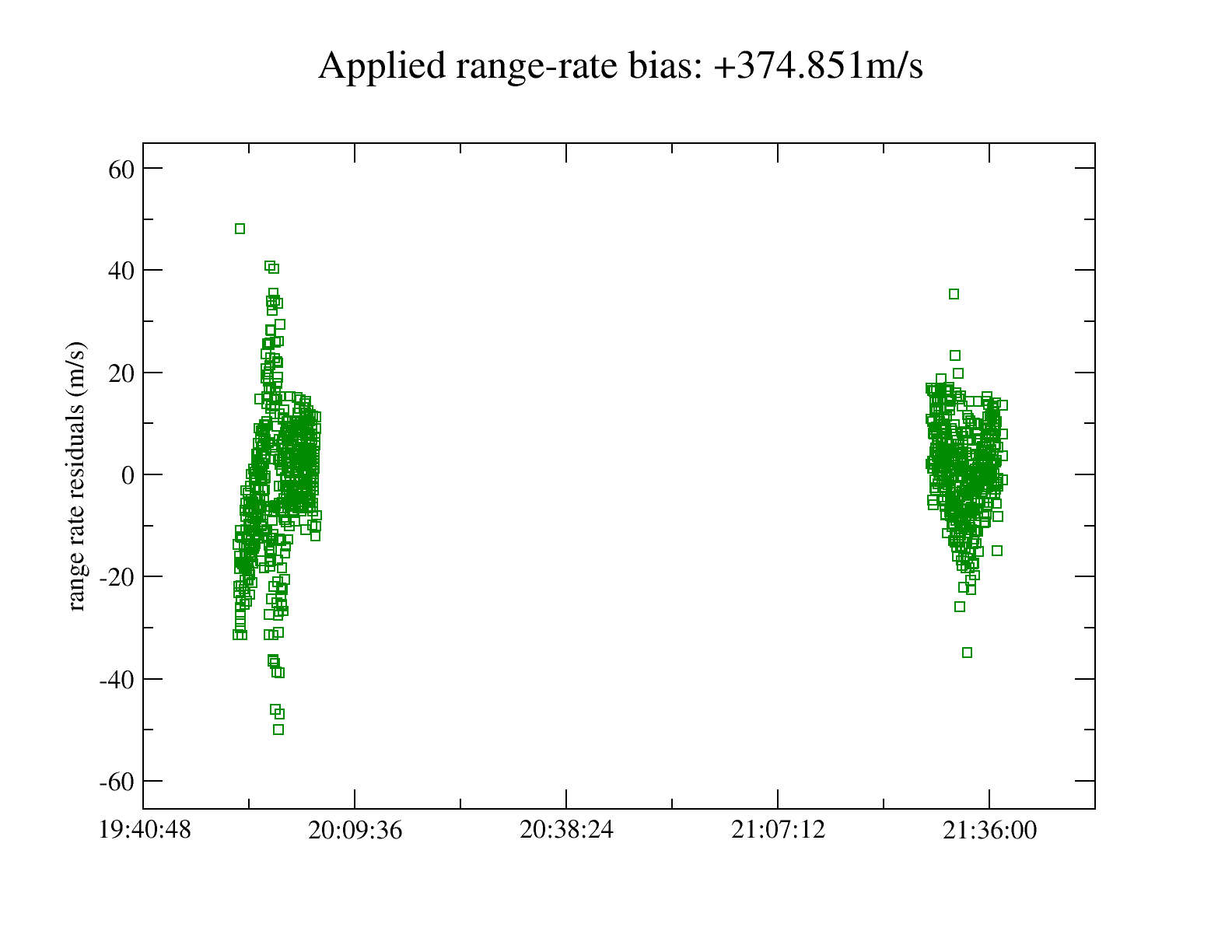
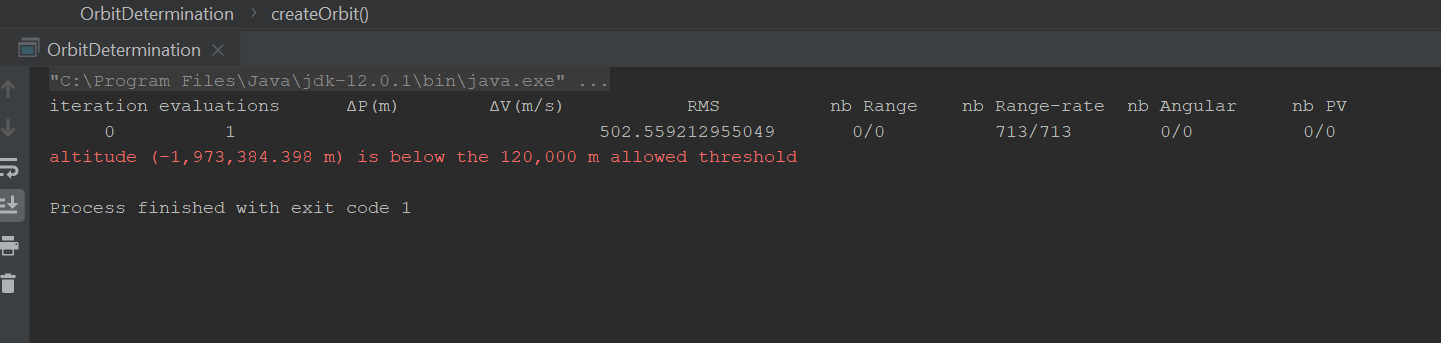
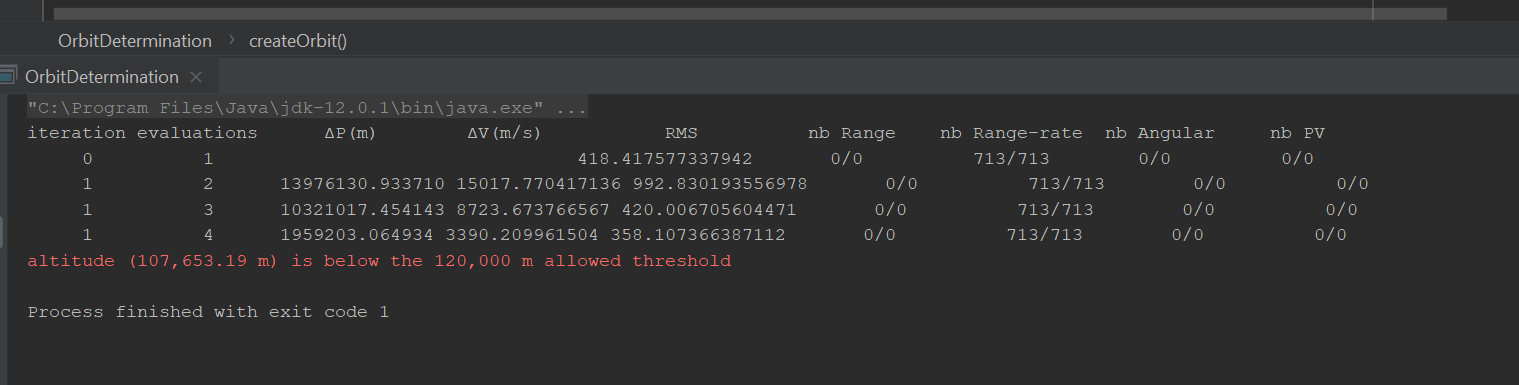
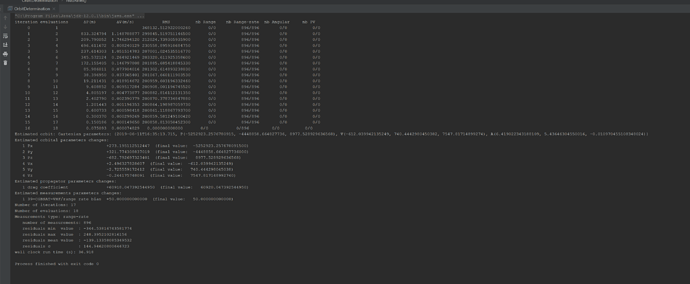
I think we are at the limit of what we can do with the current set of measurements. Playing around with the data seems to show that there are several different orbits/CD that are consistent with them. This means we have an observability problem and the various solutions are probably within a large covariance ellipsoid. Having only two passes one orbital period apart from each other and from one station only is not sufficient. The measurement noise of 15m/s is large. When we use Doppler measurements that are performed by dedicated equipment, the noise counts in centimeters or millimeters per second, not tens of meters. This was expected, as I said before, the shift we used were not designed for orbit determination.
One thing we could do is ask for more measurements. It would be nice to have several stations. Three or four stations, with as much passes over them as we can for a few orbits would be nice.
In the meantime, we can try to simulate this by ourselves, using the measurement generation feature. As the stations seem to have a large bias, we could generate our measurement sets with biases. This is done by adding another modifier to the RangeRateBuilder, either before or after having added the RangeRateTroposphericDelayModifier, as the order is irrelevant since both modifiers are additive:
final double rangeRateBias = 375.0;
builder.addModifier(new Bias<RangeRate>(new String[] { station.getBaseFrame().getName() + "-range-rate-bias" },
new double[] { rangeRateBias },
new double[] { 1.0 },
new double[] { Double.NEGATIVE_INFINITY },
new double[] { Double.POSITIVE_INFINITY }));
Of course, we should select a different, arbitrary, range-rate bias for each station as each one uses its own oscillator to generate or measure frequencies.
Concerning the model differences, I also suggest to change the measurement generator to use a numerical propagator with proper force models rather than a TLE to generate the measurements. This is done by creating the propagator first as follows:
// atmosphere model for drag
MarshallSolarActivityFutureEstimation msafe =
new MarshallSolarActivityFutureEstimation(MarshallSolarActivityFutureEstimation.DEFAULT_SUPPORTED_NAMES,
MarshallSolarActivityFutureEstimation.StrengthLevel.AVERAGE);
manager.feed(msafe.getSupportedNames(), msafe);
Atmosphere atmosphere = new DTM2000(msafe, CelestialBodyFactory.getSun(), earth);
// this orbit is a dummy one, close to the first results from orbit determination from Max Valier satellite
final NormalizedSphericalHarmonicsProvider gravity = GravityFieldFactory.getNormalizedProvider(12, 12);
final AbsoluteDate tOrb = new AbsoluteDate("2019-06-11T16:35:29.149", utc);
final TimeStampedPVCoordinates pvt = new TimeStampedPVCoordinates(tOrb,
new Vector3D(-5253194.0, -4400295.0, 80075.0),
new Vector3D(-559.0, 764.0, 7585.0));
final CartesianOrbit orbit = new CartesianOrbit(pvt, FramesFactory.getEME2000(), gravity.getMu());
final OrbitType type = OrbitType.CARTESIAN;
// set up numerical propagator
final double[][] tol = NumericalPropagator.tolerances(10.0, orbit, type);
final ODEIntegrator integrator = new DormandPrince853Integrator(0.001, 300.0, tol[0], tol[1]);
final NumericalPropagator propagator = new NumericalPropagator(integrator);
propagator.setOrbitType(type);
// add a few realistic force models
final double cd = 2.0;
final double area = 0.25;
propagator.addForceModel(new HolmesFeatherstoneAttractionModel(itrf, gravity));
propagator.addForceModel(new ThirdBodyAttraction(CelestialBodyFactory.getSun()));
propagator.addForceModel(new ThirdBodyAttraction(CelestialBodyFactory.getMoon()));
propagator.addForceModel(new DragForce(atmosphere, new IsotropicDrag(cd, area)));
Then, we should replace the propagator used by the measurement generator to remove the TLE one and use the one we just created. This is done by replacing line
final ObservableSatellite os = generator.addPropagator(TLEPropagator.selectExtrapolator(tle20190611));
by line
final ObservableSatellite os = generator.addPropagator(propagator);
Could you do these changes, check everything works and commit the generator to the forge so it remains available for everyone to see? Then you can try to generate measurements on a made-up network, putting stations where you want and choosing a different bias for each station, and perhaps also change the drag coefficient from 2.0 to some other value, say 2.7 for example so we can see if the OD can recover it starting from its initial value of 2.0. Then you can pick up in the generated measurements all or only some passes as you want, playing with the configuration to see how it affects the results. Of course, if you have lots of stations, lots of passes, you should end up with a good orbit determination (you should get back the position-velocity that were hard-coded in the measurements generation program). What is interesting are the influence of number of stations, number of passes, time span over which OD is performed, biases, drag coefficient initial error…
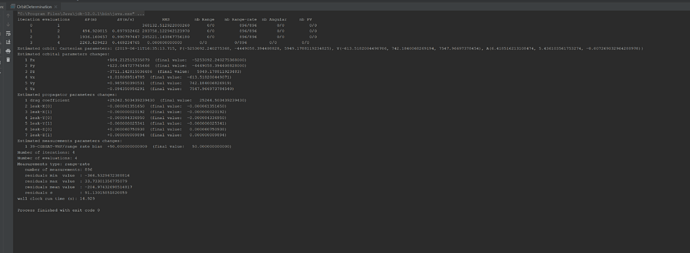
 A classical value should be around 2.0. Note that drag uses
A classical value should be around 2.0. Note that drag uses