Hello!
I’ve spent some time recently benchmarking the aforementioned (|Strict|Fast)Math classes after a coworker found our use of FastMath::sin in a particular spot was generating a huge number short-lived objects.
==================
TL;DR: in many cases, Math is faster than FastMath, and it seems unlikely that either OS or hardware makes a difference. Versions of Java different than 17 were not tested!
So, I’m wondering whether FastMath offers better numerical stability/guarantees, or whether there are other reasons to use FastMath in cases where Math is much faster.
==================
Note that I did not test all methods in these classes; I tested those that are common to each - sinCos being the sole exception (explained towards the end of this post) - intersected with those that are most commonly used in my experience.
Based on this analysis - if speed is the goal - the gist is that Math is the way to go in most cases, but Hipparchus’ FastMath should be used for the inverse and hyperbolic trig. functions (and a few others):
FastMathfaster:asin,acos,atan,atan2sinh,cosh,tanhexpm1min,max,signum
Mathfaster:sinCos,sin,cos,tanlog1p,log10,log,exphypotcbrtpowfloor,ceil,abs
Linked below is the report. The benchmarking code using JMH can be found here.
This project - Ptolemaeus - is actually a FOSS Java mathematics project that makes used of Hipparchus. It started as a “for fun” project before being incorporated into repositories at work where, after a year or two, I had it approved for FOSS release.
There are a few changes I’d still like to make before truly introducing the community to what it’s got to offer - I’d wait until v5 is released before really digging in - but the project is used in production on several high-impact programs.
Math_Benchmarks_Java17_2025-05_v3.1.0.xlsx (788.8 KB)
==================
Full Procedure
In an effort to minimize human error and to make this as portable and backwards compatible as possible:
Two Writer classes - SingleArgMathBenchmarkWriter and TwoArgMathBenchmarkWriter - were used to generate the benchmarking classes, each of which extends an abstract benchmarking class; one of SingleArgMathBenchmark and TwoArgMathBenchmark.
These JMH benchmarks are run using Gradle jmh plugin extensions:
jmhMathjmhStrictMathjmhHipparchusFastMathjmhApacheFastMath
The configuration “inherited” by each task is
jmh {
resultFormat = 'CSV' // Result format type (one of CSV, JSON, NONE, SCSV, TEXT)
warmup = '512ms' // these arga are powers of two because they're convenient
timeOnIteration = '2048ms'
iterations = 8
fork = 4
threads = Math.max(1, Runtime.getRuntime().availableProcessors() - 1)
}
To run them back-to-back, one must use more than one ./gradlew command:
./gradlew jmhMath && ./gradlew jmhStrictMath && ./gradlew jmhHipparchusFastMath && ./gradlew jmhApacheFastMath
The GitLab Runner run was performed by adding a new job to the .gitlab-ci.yml
The JMH CSV results are written to [...]\ptolemaeus\ptolemaeus-math\build\reports\jmh with names as expected: math.csv, strictMath.csv, hipparchusFastMath.csv, and apacheFastMath.csv
Once results are written, the program JMHResultsReformatter is used to reformat the results into a form more conducive to creating the Excel spreadsheets in a way that avoids human error. The first step is to write reformatted copies of each file. The second (and final) step combines the reformatted CSVs into a single combined_reformatted.csv file. The data from the combined file is copied into an Excel spreadsheet and sorted, etc.
JMHResultsReformatter takes as arguments the locations of the files to reformat and combine; e.g.,
[...]\java_math_benchmarks_2025-05\RM_home\math.csv
[...]\java_math_benchmarks_2025-05\RM_home\strictMath.csv
[...]\java_math_benchmarks_2025-05\RM_home\hipparchusFastMath.csv
[...]\java_math_benchmarks_2025-05\RM_home\apacheFastMath.csv
Before running the benchmarks, machines were restarted and nothing aside from the CLI was opened upon starting. Once started, machines were left entirely undisturbed until finished.
The machines used in benchmarking were my - referred to as “RM” - home and work machines, the work machine of a coworker of mine - referred to as “CAD” - and a GitLab Runner.
RM Work Machine Specs (DxDiag):
Operating System: Windows 11 Enterprise 64-bit (10.0, Build 22631) (22621.ni_release.220506-1250)
System Model: HP ZBook Fury 15.6 inch G8 Mobile Workstation PC
BIOS: T95 Ver. 01.20.00 (type: UEFI)
Processor: 11th Gen Intel(R) Core(TM) i9-11950H @ 2.60GHz (16 CPUs), ~2.6GHz
Available OS Memory: 32480MB RAM
RM Work JDKs:
OpenJDK 17.0.2OracleJDK 17.0.12
RM Home Machine Specs (DxDiag):
Operating System: Windows 11 Home 64-bit (10.0, Build 26100) (26100.ge_release.240331-1435)
System Model: HP ENVY Laptop 16-h1xxx
BIOS: F.22 (type: UEFI)
Processor: 13th Gen Intel(R) Core(TM) i9-13900H (20 CPUs), ~2.6GHz
Available OS Memory: 16078MB RAM
RM Home JDKs:
OpenJDK 17.0.2OracleJDK 17.0.12
CAD Work Machine Specs (DxDiag) (evidently, nearly the same):
Operating System: Windows 11 Enterprise 64-bit (10.0, Build 22631) (22621.ni_release.220506-1250)
System Model: HP ZBook Fury 15.6 inch G8 Mobile Workstation PC
BIOS: T95 Ver. 01.20.00 (type: UEFI)
Processor: 11th Gen Intel(R) Core(TM) i9-11950H @ 2.60GHz (16 CPUs), ~2.6GHz
Available OS Memory: 32432MB RAM
CAD Work JDK:
OpenJDK 17.0.2
GitLab Runner Specs:
- Definitely a Linux machine
- I’m still trying to figure this out
GitLab Runner JDK:
OpenJDK 17.0.1
==================
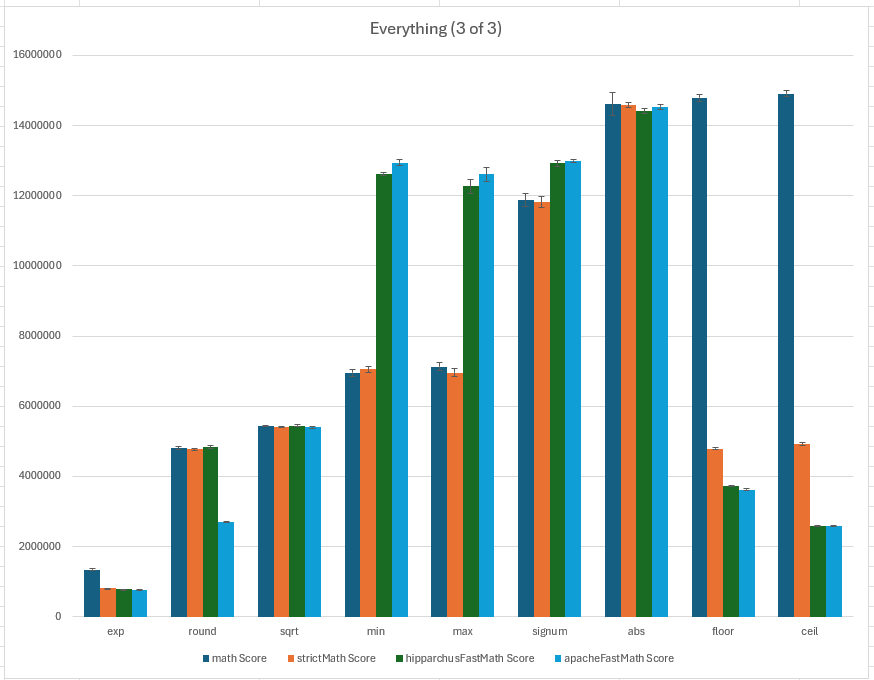
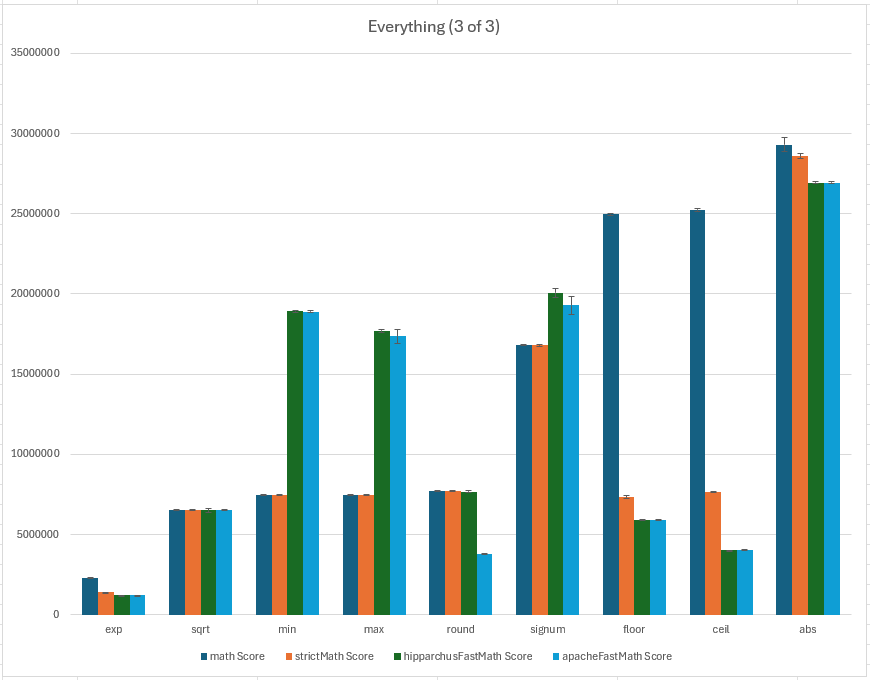
Important note regarding the y-axis values in the charts:
The “Benchmark” column shows the functions being benchmarked, but the benchmarks aren’t calling those methods just once; rather, the single-arg. functions are called 1_000 times per benchmark iteration, and the two-arg. functions are called 1_024 (== 32 * 32) times per benchmark iteration with random values chosen from intervals over which the functions are non-NaN.
E.g., the asin benchmark calls the asin methods using 1_000 values chosen randomly from [-1, 1].
The atan2 benchmark calls the atan2 methods using 1_024 (== 32 * 32) pairs of values chosen from [-10, 10]x[-10, 10].
So, the “score” is ~1000x smaller than the actual count of function calls. This does not impact the interpretation of results outside of comparing one-arg. function performance to two-arg. function performance.
General notes:
- Hipparchus
FastMathv3.1 - Apache
FastMathv3.6.1 - All Excel data originates from
JMHCSVdata, and all of that data is available (ask me - @Ryan - for it and I’ll send it out).- There is a Java script to reformat the data in a way that made it easier to paste into Excel. When run, it first creates a reformatted version of each, and then also writes a combined file. The combined file is what’s pasted into Excel.
- All trends mentioned below are approx. stable across each machine, OS, and JDK tested
- There are some differences in proportion
- By “trends” I mean - essentially - the shape of the clusters of columns for each function; e.g.:
Accounting for different orderings, these are approximately equivalent. Maybe it’s worth studying abs further, but the uncertainties are large enough that I think it’s in the noise.
Invariants/Trends:
MathvsStrictMath- For the slowest and fastest functions,
MathandStrictMathare neck-and-neck, withMathslightly ahead in general Mathis always at least as fast asStrictMath(within error bars)- Methods where
Mathfar outperformsStrictMatharesin,cos,tan,pow,log10,log,exp,ceil,floor
- For the slowest and fastest functions,
- Hipparchus
FastMathvs. ApacheFastMath- These are neck-and-neck in almost all cases, the exceptions being the combined
sinCosbenchmark andround, where Hipparchus outperformsApache
- These are neck-and-neck in almost all cases, the exceptions being the combined
Mathvs. HipparchusFastMath- In general,
FastMathis only faster thanMathfor the slowest functions, as well asminandmax, strangely enough. Mathapprox. equalFastMathroundsqrtsqrtis easily the most consistent among all functions benchmarked. All four classes tie - within uncertainty - in each case.
FastMathfaster:asinacosatanatan2sinhcoshtanhexpm1minmaxsignum
Mathfaster:log1psinCos(I elaborate below)powsincostancbrtlog10hypotlogexpfloorceilabs
- In general,
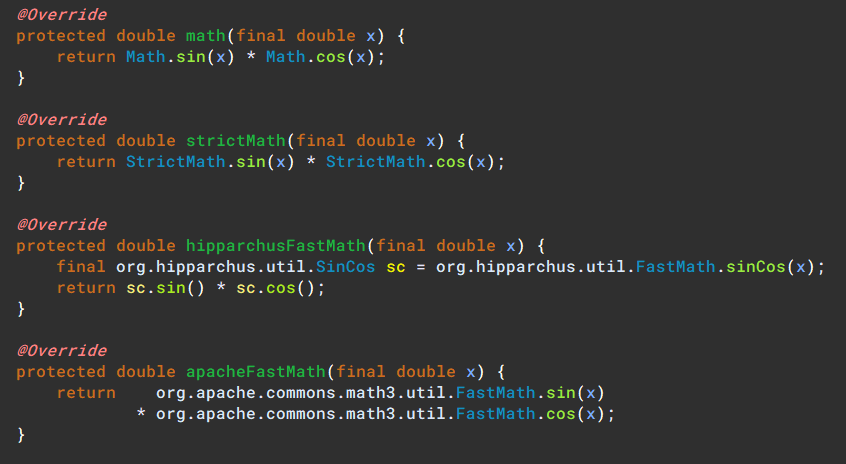
This screenshot is representative of results overall:
Specific cases of note:
sinCos- Only Hipparchus’
FastMathhassinCos - To compare, those without simply compute
sinandcosseparately
- Only Hipparchus’