Hello,
I have some problems with DSSTPropagator using, so I’ll be very grateful for your help.
My purpose is to propagate LEO satellite orbit for long periods, so I found recommendations about using DSSTPropagator for such calculations.
I used examples and tests and wrote a code, but the results of calculations are quite different from the same calculations, made with numerical propagator or in GMAT.
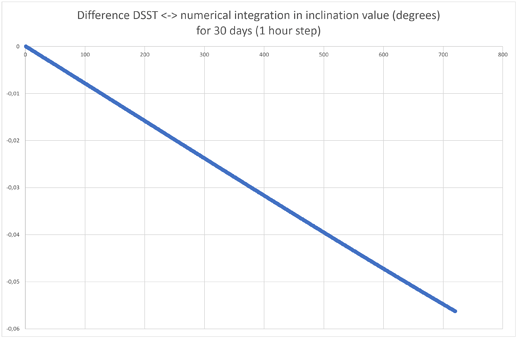
The differences are about x00 metres in semi-major axis and about 0.0x degrees in inclination for 10 - 30 days. I understand, that it’s incorrect to compare position-velocity components, so I compare orbit elements. I tried different combinations of “mean/osculating” tunings, but in all cases the difference seems to be too big.
At the beginning I used model with many forces (Earth gravity, Moon and Sun gravity, atmospheric drag), but I noticed, that the problem appears with the Earth gravity (the results for DSST and numerical integration are the same for spheric Earth gravity field, but there is a difference for 2 x 0 and further).
I examined all the tunings about constants, coordinate systems, etc., but I have no idea, how to explain such a difference. (I tried both position-velocity or keplerian orbit for initial SpacecraftState, nothing changed.)
Here is my code.
File orekitData = new File("C:\\tempForOrekit");
DataContext.getDefault().getDataProvidersManager().addProvider(new DirectoryCrawler(orekitData));
AbsoluteDate initialDate = new AbsoluteDate(
2020, 3, 12, 4, 37, 0, TimeScalesFactory.getUTC());
PVCoordinates pvCoordinates = new PVCoordinates(
new Vector3D(6823.698321e+3, -952.003960e+3, -13.187505e+3),
new Vector3D(-0.131194e+3, -0.976418e+3, 7.543914e+3));
Frame inertialFrame = FramesFactory.getEME2000();
KeplerianOrbit initialOrbit = new KeplerianOrbit(
6893.081283931438e+3,
0.001331122212474694,
Math.toRadians(97.44029236157961),
Math.toRadians(69.0070994141481),
Math.toRadians(352.0433593955477),
Math.toRadians(290.8823016332061),
PositionAngle.TRUE,
inertialFrame, initialDate, Constants.EGM96_EARTH_MU);
final SpacecraftState initialState = new SpacecraftState(initialOrbit);
// Initialize the DSST propagator
final double minStep = initialState.getKeplerianPeriod();
final double maxStep = 100. * minStep;
final double[][] tol = DSSTPropagator.tolerances(1.0, initialState.getOrbit());
final AdaptiveStepsizeIntegrator integrator = new DormandPrince853Integrator(minStep, maxStep, tol[0], tol[1]);
final DSSTPropagator dsstProp = new DSSTPropagator(integrator, PropagationType.OSCULATING);
dsstProp.setInitialState(initialState, PropagationType.OSCULATING);
// Central Body geopotential 2x0 (J2 only)
final UnnormalizedSphericalHarmonicsProvider provider = GravityFieldFactory.getUnnormalizedProvider(2, 0);
final OneAxisEllipsoid earth = new OneAxisEllipsoid(provider.getAe(),
Constants.WGS84_EARTH_FLATTENING,
FramesFactory.getITRF(IERSConventions.IERS_2010, true));
// Add the force models to the propagator
dsstProp.addForceModel(new DSSTZonal(provider));
dsstProp.addForceModel(new DSSTTesseral(earth.getBodyFrame(), Constants.WGS84_EARTH_ANGULAR_VELOCITY, provider));
// 10 days propagation
final SpacecraftState finalState = dsstProp.propagate(initialDate.shiftedBy(10. * Constants.JULIAN_DAY));
PVCoordinates pv = finalState.getPVCoordinates(inertialFrame);
Orbit orbit = new KeplerianOrbit(pv, inertialFrame, finalState.getDate(), Constants.EGM96_EARTH_MU);
double aM = orbit.getA();
double e = orbit.getE();
double iDegrees = Math.toDegrees(orbit.getI());
// reference data from GMAT:
// Cartesian State Keplerian State
// --------------------------- --------------------------------
// X = 2617.7180296979 km SMA = 6877.0840271856 km
// Y = 916.41629724835 km ECC = 0.0022472704215
// Z = -6308.9965773698 km INC = 97.468200487389 deg
// VX = 7.0209016138680 km/sec RAAN = 1.9452039595408 deg
// VY = -0.1417284428202 km/sec AOP = 93.814590070776 deg
// VZ = 2.8985288247191 km/sec TA = 198.77517269129 deg
// MA = 198.85818878177 deg
// EA = 198.81665869991 deg
assertEquals(6877.0840271856e+3, aM, 1); // got 6877039.514159619
assertEquals(0.0022472704215, e, 1e-6); // got 0.002250298057808621
assertEquals(97.468200487389, iDegrees, 1e-6); // got 97.44902204199919
Thank you in advance for your answers.