Hi Orekit community!
I’m completly new to Orekit and have absolutely no experience in Java which is not helping. I’m dealing with a problem: I want to make a pipeline that given input as position and velocity vectors in ITRF will firstly make IOD and then fit this IOD to the rest of positions to construct orbit. So far I have encountered numerous obstacles and I can’t really wrap my head around them.
First I have tried using iod_gibbs for my initial orbit determination but it gave me this error:
JavaError: <super: <class 'JavaError'>, <JavaError object>>
Java stacktrace:
org.orekit.errors.OrekitIllegalArgumentException: non pseudo-inertial frame "CIO/2010-based ITRF accurate EOP"
at org.orekit.orbits.Orbit.ensurePseudoInertialFrame(Orbit.java:202)
at org.orekit.orbits.Orbit.<init>(Orbit.java:141)
at org.orekit.orbits.KeplerianOrbit.<init>(KeplerianOrbit.java:313)
at org.orekit.orbits.KeplerianOrbit.<init>(KeplerianOrbit.java:291)
at org.orekit.orbits.KeplerianOrbit.<init>(KeplerianOrbit.java:422)
at org.orekit.estimation.iod.IodGibbs.estimate(IodGibbs.java:143)
at org.orekit.estimation.iod.IodGibbs.estimate(IodGibbs.java:86)
I’ve infered that I need to use other, pseudo-inertial frame. Is there a way to estimate IOD using ITRF?
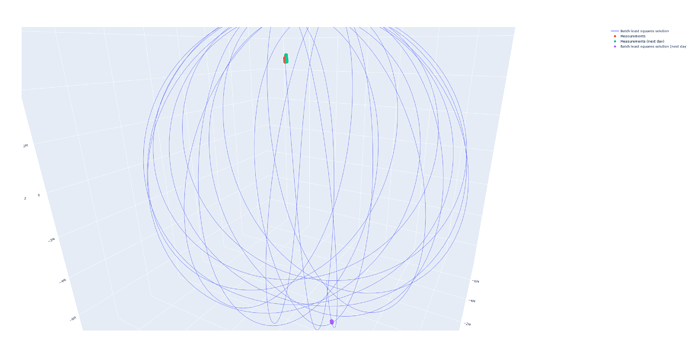
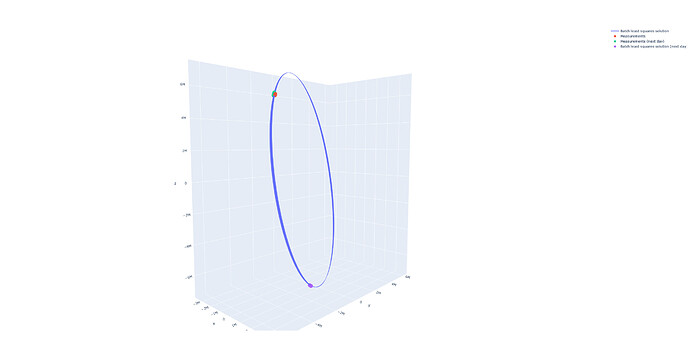
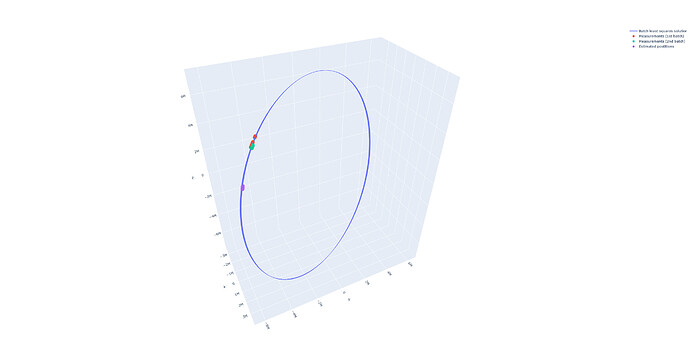
Second, I have transformed three vectors to GCRF and IOD was created, albeit very inaccurate:
import math
i = math.ceil(len(dane.index) / 3)
points_for_iod = data.iloc[::i, :]
display(points_for_iod)
from org.hipparchus.geometry.euclidean.threed import Vector3D
from orekit.pyhelpers import datetime_to_absolutedate
from org.orekit.utils import PVCoordinates
from org.orekit.estimation.measurements import PV
pos_1 = points_for_iod.iloc[0]
p_vector_1 = Vector3D(pos_1[['x_', 'y_', 'z_']].to_list())
v_vector_1 = Vector3D(pos_1[["vx_", "vy_", "vz_"]].to_list())
date_1 = datetime_to_absolutedate(points_for_iod.index[0])
tmp_pv1 = PVCoordinates(p_vector_1, v_vector_1)
pv1 = itrf.getTransformTo(gcrf, date_1).transformPVCoordinates(tmp_pv1)
pos_2 = points_for_iod.iloc[1]
p_vector_2 = Vector3D(pos_2[['x_', 'y_', 'z_']].to_list())
v_vector_2 = Vector3D(pos_2[["vx_", "vy_", "vz_"]].to_list())
date_2 = datetime_to_absolutedate(points_for_iod.index[1])
tmp_pv2 = PVCoordinates(p_vector_2, v_vector_2)
pv2 = itrf.getTransformTo(gcrf, date_2).transformPVCoordinates(tmp_pv2)
pos_3 = points_for_iod.iloc[2]
p_vector_3 = Vector3D(pos_3[['x_', 'y_', 'z_']].to_list())
v_vector_3 = Vector3D(pos_3[["vx_", "vy_", "vz_"]].to_list())
date_3 = datetime_to_absolutedate(points_for_iod.index[2])
tmp_pv3 = PVCoordinates(p_vector_3, v_vector_3)
pv3 = itrf.getTransformTo(gcrf, date_3).transformPVCoordinates(tmp_pv3)
from org.orekit.estimation.iod import IodGibbs
from org.orekit.utils import Constants as orekit_constants
iod_gibbs = IodGibbs(orekit_constants.EIGEN5C_EARTH_MU)
initialOrbit = iod_gibbs.estimate(gcrf,
pv1.getPosition(), date_1,
pv2.getPosition(), date_2,
pv3.getPosition(), date_3)
Next obstacle appeared when I tried to propagate this orbit:
prop_min_step = 0.001 # s
prop_max_step = 300.0 # s
prop_position_error = 5000.0 # m
estimator_position_scale = 1.0 # m
estimator_convergence_thres = 1e-2
estimator_max_iterations = 75
estimator_max_evaluations = 100
from org.orekit.propagation.conversion import DormandPrince853IntegratorBuilder
integratorBuilder = DormandPrince853IntegratorBuilder(prop_min_step, prop_max_step, prop_position_error)
from org.orekit.propagation.conversion import NumericalPropagatorBuilder
from org.orekit.orbits import PositionAngle
propagatorBuilder = NumericalPropagatorBuilder(initialOrbit,
integratorBuilder,
PositionAngle.TRUE,
estimator_position_scale)
from org.hipparchus.linear import QRDecomposer
matrix_decomposer = QRDecomposer(1e-11)
from org.hipparchus.optim.nonlinear.vector.leastsquares import GaussNewtonOptimizer
optimizer = GaussNewtonOptimizer(matrix_decomposer, False)
from org.orekit.estimation.leastsquares import BatchLSEstimator
estimator = BatchLSEstimator(optimizer, propagatorBuilder)
estimator.setParametersConvergenceThreshold(estimator_convergence_thres)
estimator.setMaxIterations(estimator_max_iterations)
estimator.setMaxEvaluations(estimator_max_evaluations)
from org.orekit.estimation.measurements import Position, ObservableSatellite
observableSatellite = ObservableSatellite(0) # Propagator index = 0
for timestamp, pv_gcrf in data.iterrows():
tmp_p = Vector3D(pv_gcrf[['x_', 'y_', 'z_']].to_list())
tmp_v = Vector3D(pv_gcrf[['vx_', 'vy_', 'vz_']].to_list())
tmp_pvc = PVCoordinates(tmp_p, tmp_v)
pvc = itrf.getTransformTo(gcrf, datetime_to_absolutedate(timestamp)).transformPVCoordinates(tmp_pvc)
orekit_position = Position(
datetime_to_absolutedate(timestamp),
pvc.getPosition(),
1000.0,
1.0, # Base weight
observableSatellite
)
estimator.addMeasurement(orekit_position)
estimatedPropagatorArray = estimator.estimate()
This resulted in error:
JavaError: <super: <class 'JavaError'>, <JavaError object>>
Java stacktrace:
org.orekit.errors.OrekitException: Jacobian matrix for type KEPLERIAN is singular with current orbit
at org.orekit.propagation.numerical.NumericalPropagator.tolerances(NumericalPropagator.java:1081)
at org.orekit.propagation.numerical.NumericalPropagator.tolerances(NumericalPropagator.java:1025)
at org.orekit.propagation.conversion.DormandPrince853IntegratorBuilder.buildIntegrator(DormandPrince853IntegratorBuilder.java:55)
at org.orekit.propagation.conversion.NumericalPropagatorBuilder.buildPropagator(NumericalPropagatorBuilder.java:206)
at org.orekit.propagation.conversion.NumericalPropagatorBuilder.buildPropagator(NumericalPropagatorBuilder.java:46)
at org.orekit.estimation.leastsquares.AbstractBatchLSModel.createPropagators(AbstractBatchLSModel.java:419)
at org.orekit.estimation.leastsquares.AbstractBatchLSModel.value(AbstractBatchLSModel.java:298)
at org.hipparchus.optim.nonlinear.vector.leastsquares.LeastSquaresFactory$LocalLeastSquaresProblem.evaluate(LeastSquaresFactory.java:440)
at org.orekit.estimation.leastsquares.BatchLSEstimator$TappedLSProblem.evaluate(BatchLSEstimator.java:615)
at org.hipparchus.optim.nonlinear.vector.leastsquares.GaussNewtonOptimizer.optimize(GaussNewtonOptimizer.java:163)
at org.orekit.estimation.leastsquares.BatchLSEstimator.estimate(BatchLSEstimator.java:435)
I’ve found somewhere in this forum that you can work around this error by changing orbity type to cartesian. So I’ve changed the code:
initialCartOrbit = OrbitType.CARTESIAN.convertType(initialOrbit)
propagatorBuilder = NumericalPropagatorBuilder(initialCartOrbit,
integratorBuilder,
PositionAngle.TRUE,
estimator_position_scale)
and it kinda worked. My last step was getting estimated Keplerian orbit:
dt = 1.0
date_start = datetime_to_absolutedate(dane.index[0])
date_end = datetime_to_absolutedate(dane.index[-1])
estimatedPropagator = estimatedPropagatorArray[0]
estimatedInitialState = estimatedPropagator.getInitialState()
orbit = OrbitType.KEPLERIAN.convertType(estimatedInitialState.getOrbit())
Using this I’ve gotten pretty accurate orbit. RAAN, e and i are pretty spot on, a is 3 km bigger then truth but that’s okay for now.
Last problems that I don’t know how to deal with is why I cant set ephmeris mode to this estimated propagator and why this orbit has no attributes like " getPerigeeArgument()" or “getRightAscensionOfAscendingNode()”
In summary, is there a better way of performing IOD and OD with ITRF data that I have? Maybe a way that has none of the problems mentioned above?