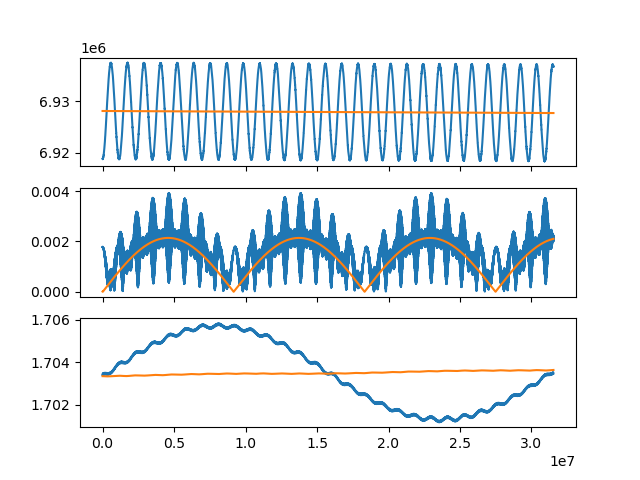
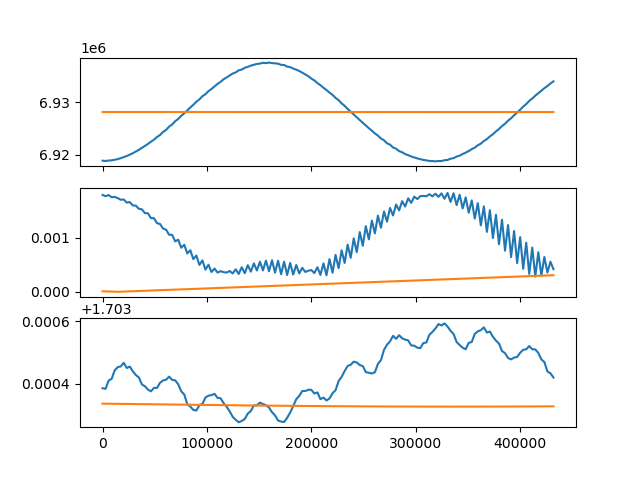
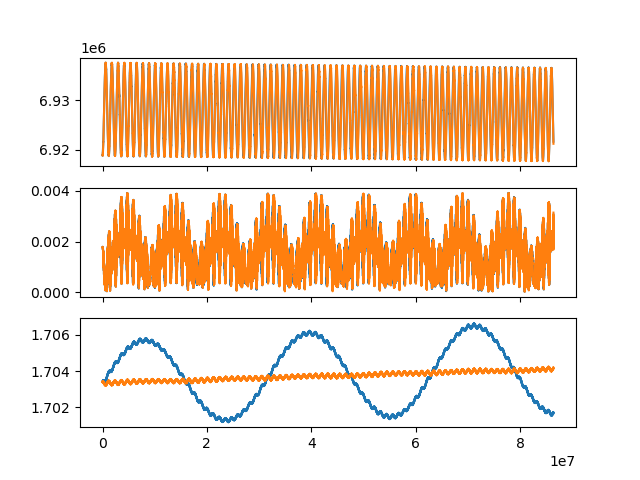
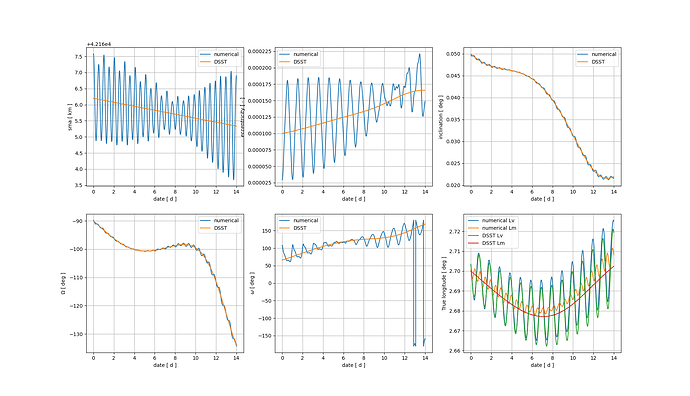
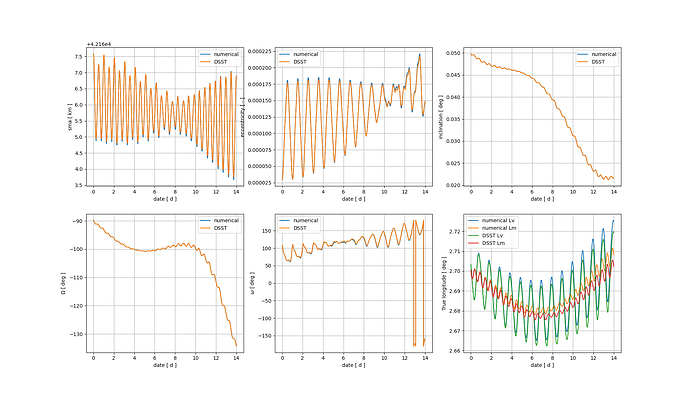
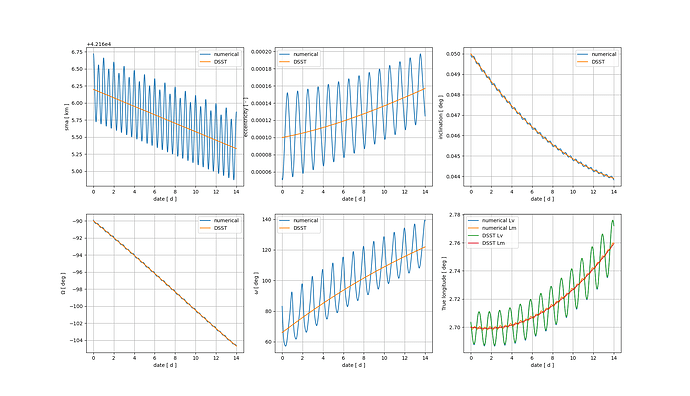
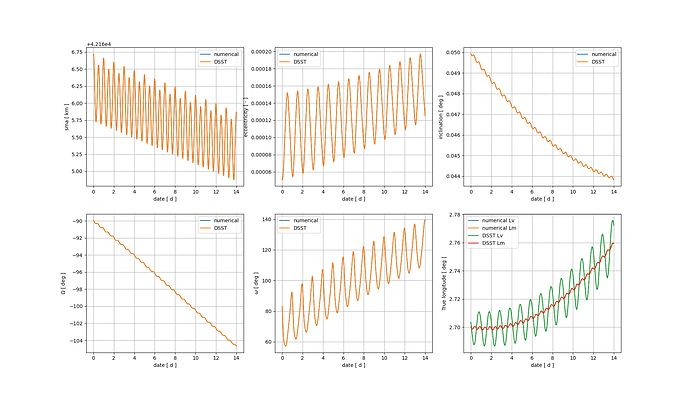
I tried using the frame you suggested but I still get the same results.
Here is my code, maybe that way it can be easier to locate a possible error:
n, m = 4, 4;
gravityProvider = GravityFieldFactory.getConstantNormalizedProvider(n,m);
nonSphericalGravity = HolmesFeatherstoneAttractionModel(CelestialBodyFactory.getEarth().getBodyOrientedFrame(), gravityProvider);
forces = [nonSphericalGravity];
gravityProviderDsst = GravityFieldFactory.getConstantUnnormalizedProvider(n,m);
zonalDsst = DSSTZonal(gravityProviderDsst);
tesseralDsst = DSSTTesseral(CelestialBodyFactory.getEarth().getBodyOrientedFrame(),
Constants.WGS84_EARTH_ANGULAR_VELOCITY,
gravityProviderDsst);
forcesDsst = [zonalDsst, tesseralDsst];
minStep = 1e-2;
maxStep = 1e+3;
absTol = 1e-9;
relTol = 1e-9;
integrator = DormandPrince853Integrator(minStep, maxStep, absTol, relTol);
integrator.setInitialStepSize(60.0);
propagator = NumericalPropagator(integrator);
propagator.setResetAtEnd(False);
propagator.setAttitudeProvider(earthCenterAttitudeLaw);
for force in forces:
propagator.addForceModel(force);
ephGen = propagator.getEphemerisGenerator();
initOrbitMean = KeplerianOrbit(a0, e0, i0, pa0, raan0, f0, PositionAngle.TRUE,
FramesFactory.getEME2000(), initDate, Constants.WGS84_EARTH_MU);
initStateMean = SpacecraftState(initOrbitMean, mass);
integratorDsst = ClassicalRungeKuttaIntegrator(10*initOrbitMean.getKeplerianPeriod());
propagatorDsst = DSSTPropagator(integratorDsst, PropagationType.MEAN);
propagatorDsst.setResetAtEnd(False);
for force in forcesDsst:
propagatorDsst.addForceModel(force);
ephGenDsst = propagatorDsst.getEphemerisGenerator();
initStateOsc = propagatorDsst.computeOsculatingState(initStateMean, earthCenterAttitudeLaw, propagatorDsst.getAllForceModels());
propagator.setInitialState(initStateOsc);
propagatorDsst.setInitialState(initStateMean, PropagationType.MEAN);
nDays = 14;
tSpan = nDays*day;
finalDate = initDate.shiftedBy(tSpan);
propagator.propagate(finalDate);
print("NumericalPropagator done");
propagatorDsst.propagate(finalDate);
print("DSSTPropagator done");
timeVec = linspace(0, tSpan, 30*nDays);
aOsc, eOsc, iOsc = [], [], [];
aMean, eMean, iMean = [], [], [];
for time in timeVec:
dateNow = initDate.shiftedBy(float(time));
pvOsc = ephGen.getGeneratedEphemeris().getPVCoordinates(dateNow, FramesFactory.getEME2000());
pvMean = ephGenDsst.getGeneratedEphemeris().getPVCoordinates(dateNow, FramesFactory.getEME2000());
orbitOsc = KeplerianOrbit(pvOsc, FramesFactory.getEME2000(), Constants.WGS84_EARTH_MU);
orbitMean = KeplerianOrbit(pvMean, FramesFactory.getEME2000(), Constants.WGS84_EARTH_MU);
aOsc.append(orbitOsc.getA());
eOsc.append(orbitOsc.getE());
iOsc.append(orbitOsc.getI());
aMean.append(orbitMean.getA());
eMean.append(orbitMean.getE());
iMean.append(orbitMean.getI());