Hi Maxime and thank you for your quick answer 
Yes, I consider keplerian elements to be my mean elements (they should be the mean elements, aren’t they?).
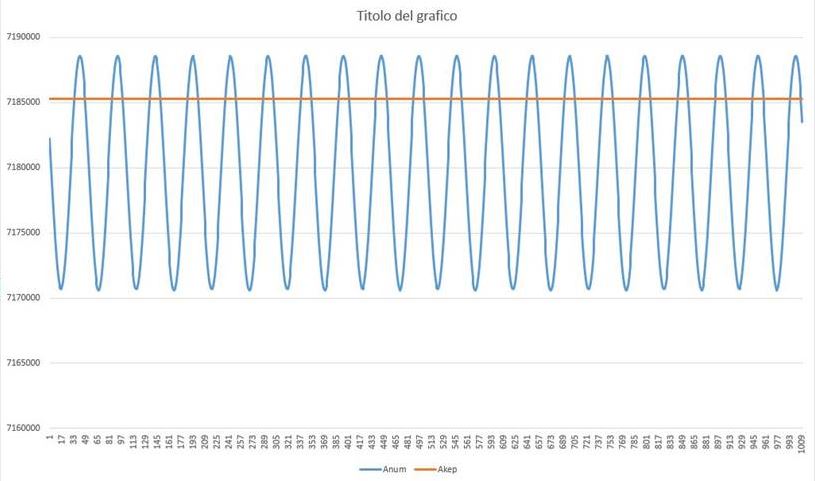
The idea is to use a numerical propagator with a full force model, and than to convert the propagator into a keplerian so that I can obtain the keplerian (constant) orbital parameters.
Hereafter I attached the code that produces the results of the previous figure:
public class PropagatorConversion {
public static void main(String[] args) {
//Configuration data//
File orekitData = new File("orekit-data");
DataProvidersManager manager = DataProvidersManager.getInstance();
manager.addProvider(new DirectoryCrawler(orekitData));
//////////////////////
// gravity field
NormalizedSphericalHarmonicsProvider provider = GravityFieldFactory.getNormalizedProvider(2, 0);
double mu = provider.getMu();
// inertial frame
Frame inertialFrame = FramesFactory.getEME2000();
// Initial date
AbsoluteDate initialDate = new AbsoluteDate(2022,11,01,1,48,9.303,
TimeScalesFactory.getUTC());
// Initial orbit
final double a = 7182.25536152*1000; // semi major axis in meters
final double e = 0.00111776; // eccentricity
final double i = FastMath.toRadians(98.73774250); // inclination
final double omega = FastMath.toRadians(65.11464822); // perigee argument
final double raan = FastMath.toRadians(2.23553023); // right ascention of ascending node
final double TA = FastMath.toRadians(151.17294416); // true anomaly
Orbit initialOrbit = new KeplerianOrbit(a, e, i, omega, raan, TA, PositionAngle.TRUE,
inertialFrame, initialDate, mu);
final double period = initialOrbit.getKeplerianPeriod();
// Initial state definition
final SpacecraftState initialState = new SpacecraftState(initialOrbit);
// Adaptive step integrator with a minimum step of 0.001 and a maximum step of 1000
final double minStep = 0.001;
final double maxStep = 1000.;
final double dP = 1.e-2;
final OrbitType orbType = OrbitType.CARTESIAN;
final double[][] tol = NumericalPropagator.tolerances(dP, initialOrbit, orbType);
final AbstractIntegrator integrator = new DormandPrince853Integrator(minStep, maxStep,
tol[0], tol[1]);
// Propagator
NumericalPropagator numProp = new NumericalPropagator(integrator);
numProp.setInitialState(initialState);
numProp.setOrbitType(orbType);
//Propagator Force Model////////////////////////////////////////////////////////////////////////////////////////////////// //
//1) Gravity Field & Third Body //
//
ForceModel holmesFeatherstone = //
new HolmesFeatherstoneAttractionModel(FramesFactory.getITRF(IERSConventions.IERS_2010,true),provider); //
numProp.addForceModel(holmesFeatherstone); //
numProp.addForceModel(new ThirdBodyAttraction(CelestialBodyFactory.getSun())); //
numProp.addForceModel(new ThirdBodyAttraction(CelestialBodyFactory.getMoon())); //
//
//2) Drag //
final DragForce drag = //
new DragForce(new HarrisPriester(CelestialBodyFactory.getSun(), //
new OneAxisEllipsoid(Constants.WGS84_EARTH_EQUATORIAL_RADIUS, //
Constants.WGS84_EARTH_FLATTENING, //
FramesFactory.getITRF(IERSConventions.IERS_2010, true))), //
new IsotropicDrag(2.5, 1.2)); //
numProp.addForceModel(drag); //
//
//3) Solar Radiation Pressure //
ExtendedPVCoordinatesProvider sun = CelestialBodyFactory.getSun(); //
OneAxisEllipsoid earth = //
new OneAxisEllipsoid(6378136.46, 1.0 / 298.25765, //
FramesFactory.getITRF(IERSConventions.IERS_2010, true)); // //
SolarRadiationPressure SRP = //
new SolarRadiationPressure(sun, earth.getEquatorialRadius(), //
(RadiationSensitive) new IsotropicRadiationSingleCoefficient(1.2, 1.2)); //
numProp.addForceModel(SRP); //
//////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////
// Propagator factory
PropagatorBuilder builder = new KeplerianPropagatorBuilder(initialOrbit, PositionAngle.TRUE, dP);
// Propagator converter
PropagatorConverter fitter = new FiniteDifferencePropagatorConverter(builder, 1.e-6, 5000);
// Resulting propagator
KeplerianPropagator kepProp = (KeplerianPropagator)fitter.convert(numProp, 2*period, 251);
// Step handlers
StatesHandler numStepHandler = new StatesHandler();
StatesHandler kepStepHandler = new StatesHandler();
// Set up operating mode for the propagator as master mode
// with fixed step and specialized step handler
numProp.setMasterMode(60., numStepHandler);
kepProp.setMasterMode(60., kepStepHandler);
// Extrapolate from the initial to the final date
numProp.propagate(initialDate, initialDate.shiftedBy(10.*period));
kepProp.propagate(initialDate, initialDate.shiftedBy(10.*period));
// retrieve the states
List<SpacecraftState> numStates = numStepHandler.getStates();
List<SpacecraftState> kepStates = kepStepHandler.getStates();
// Print the results on the output file
System.out.println("Mean SMA (constant):"+ kepProp.getInitialState().getA());
System.out.println("");
System.out.println("Osculating SMA");
for (SpacecraftState numState : numStates) {
for (SpacecraftState kepState : kepStates) {
if (numState.getDate().compareTo(kepState.getDate()) == 0) {
System.out.println(numState.getA());
break;
}
}
}
}
/** Specialized step handler.
* <p>This class extends the step handler in order to handle states at each step.<p>
*/
private static class StatesHandler implements OrekitFixedStepHandler {
/** Points. */
private final List<SpacecraftState> states;
public StatesHandler() {
// prepare an empty list of SpacecraftState
states = new ArrayList<SpacecraftState>();
}
public void handleStep(SpacecraftState currentState, boolean isLast) {
// add the current state
states.add(currentState);
}
/** Get the list of handled orbital elements.
* @return orbital elements list
*/
public List<SpacecraftState> getStates() {
return states;
}
}
}
I will see also the DSST propagator, as you suggested.
Thank you!!
Giacomo
? Remember that this close to Earth, Keplerian motion is really really far from reality. At least it will not allow your orbital plane to follow Sun, so you will gets tens of kilometers mismatch with reality very soon. Perhaps you could try to convert not to Keplerian but to something still simple but more realistic like Eckstein-Hechler?