Hello,
is there a way to use orekit in order to propagate an orbit and perform station keeping manoeuvres whenever the spacecraft position is outside of a given boundary from the nominal orbit (due to drag in LEO, for example)? Which methods should I adopt in my code, in addition to the basic ones for propagation?
Thanks in advance.
Hi @a_gior,
Orekit doesn’t provide ad hoc station-keeping methods, but it does offer all the components needed to build them … with a bit of work.
You can have a look at the tutorials, (in java) and in particular the maneuvers package, which offers three applications related to orbit control. The StationKeeping tutorial, which deals with east/west station-keeping in GEO, i.e. in a longitude window, may give you an idea of the specific developments required.
Dear @pascal.parraud,
thank you for your reply. Before going deep in the maneuvers package, I wanted to make sure that I am correctly monitoring the displacement with respect to the nominal orbit, which should afterwards trigger a corrective manoeuvre.
For this reason I am actually considering the semi-major axis variation only, for now, and I am evaluating the difference between a numerically propagated orbit without drag and a numerically propagated orbit with drag, as can be seen in the code below:
year = 2026
month = 1
day = 1
hour = 6
minute = 0
seconds = 0.0
date_propagation = '2026-01-01T06:00:00.000'
duration = 24*60*60*7 # Propagation duration [s]
step_time = 50. # Propagation step-time [s]
J2 = -Constants.EIGEN5C_EARTH_C20
a = 6860. * 1000 # Orbit semi-major axis [m]
e = 0.0 # Orbit eccentricity [-]
mu_e = Constants.EIGEN5C_EARTH_MU # Earth gravitational parameter [kg*m^3/s^2]
R_e = Constants.WGS84_EARTH_EQUATORIAL_RADIUS # Earth equatorial radius [m]
i = radians(97.3) # Orbit inclination [rad]
omega = radians(90.0) # Orbit perigee argument [rad]
raan = radians(10.0) # Orbit LTAN [h]
true_anomaly = radians(45.0) # Spacecraft true anomaly [rad]
utc = TimeScalesFactory.getUTC() # Define UTC time-scale
epochDate = AbsoluteDate(year, month, day, hour, minute, seconds, utc) # Propagation start-time [s]
epoch = Time(date_propagation) # Propagation start-time [s]
sun = CelestialBodyFactory.getSun() # Create sun in simulation
inertialFrame = FramesFactory.getEME2000()
utc = TimeScalesFactory.getUTC() # Define UTC time-scale
epochDate = AbsoluteDate(year, month, day, hour, minute, seconds, utc) # Propagation start-time [s]
sun = CelestialBodyFactory.getSun() # Create sun in simulation
# Initial orbit definition, spacecraft in the middle of the formation
initialOrbit = KeplerianOrbit(a, e, i, omega, raan, true_anomaly,
PositionAngle.TRUE,
inertialFrame, epochDate, Constants.EIGEN5C_EARTH_MU)
satellite_mass = 37. # Spacecraft mass [kg]
# Numerical propagator definition
# Step size
minStep = 0.001
maxStep = step_time.
initStep = step_time
positionTolerance = 1E-3
propagationType = OrbitType.CARTESIAN
tolerances = NumericalPropagator.tolerances(positionTolerance, initialOrbit, propagationType)
# Middle spacecraft numerical propagator
integrator = DormandPrince853Integrator(minStep, maxStep, orekit.JArray('double').cast_(tolerances[0]), orekit.JArray('double').cast_(tolerances[1]))
integrator.setInitialStepSize((initStep))
numericalPropagator = NumericalPropagator(integrator)
numericalPropagator.setOrbitType(propagationType)
itrf = FramesFactory.getITRF(IERSConventions.IERS_2010, True) # International Terrestrial Reference Frame, earth fixed
earth = OneAxisEllipsoid(Constants.WGS84_EARTH_EQUATORIAL_RADIUS,
Constants.WGS84_EARTH_FLATTENING,
itrf)
gravityProvider1 = GravityFieldFactory.getNormalizedProvider(60, 60)
numericalPropagator.addForceModel(HolmesFeatherstoneAttractionModel(earth.getBodyFrame(), gravityProvider1))
numericalPropagator.setInitialState(SpacecraftState(initialOrbit, satellite_mass))
# First spacecraft numerical propagator
tolerances2 = NumericalPropagator.tolerances(positionTolerance, initialOrbit2, propagationType)
integrator2 = DormandPrince853Integrator(minStep, maxStep, orekit.JArray('double').cast_(tolerances2[0]), orekit.JArray('double').cast_(tolerances2[1]))
integrator2.setInitialStepSize((initStep))
numericalPropagator2 = NumericalPropagator(integrator2)
numericalPropagator2.setOrbitType(propagationType)
gravityProvider2 = GravityFieldFactory.getNormalizedProvider(60, 60)
numericalPropagator2.addForceModel(HolmesFeatherstoneAttractionModel(earth.getBodyFrame(), gravityProvider2))
numericalPropagator2.setInitialState(SpacecraftState(initialOrbit2, satellite_mass))
crossSection_drag2 = 0.35 #m2
dragCoeff = 2.2 # Spacecraft drag coefficient
# Initialize drag perturbation
strenghtLevel = MarshallSolarActivityFutureEstimation.StrengthLevel.AVERAGE
supportedNames = MarshallSolarActivityFutureEstimation.DEFAULT_SUPPORTED_NAMES
inputParameters_Drag = MarshallSolarActivityFutureEstimation(supportedNames, strenghtLevel)
atmosphere = NRLMSISE00(inputParameters_Drag, sun, earth)
spacecraftDrag2 = IsotropicDrag(crossSection_drag2, dragCoeff)
drag2 = DragForce(atmosphere, spacecraftDrag2)
numericalPropagator2.addForceModel(drag2)
# Moon and Sun third-body perturbations
moon = CelestialBodyFactory.getMoon()
sun = CelestialBodyFactory.getSun()
moon_3dbodyattraction = ThirdBodyAttraction(moon)
numericalPropagator2.addForceModel(moon_3dbodyattraction)
sun_3dbodyattraction = ThirdBodyAttraction(sun)
numericalPropagator2.addForceModel(sun_3dbodyattraction)
# Spacecraft cross section used for Solar Radiation Pressure perturbation
crossSection_SRP = 1.45 #m2
reflectivityCoeff = 1.3 # Spacecraft reflectivity coefficient
# Initialize SRP perturbation model
spacecraftSRP = IsotropicRadiationSingleCoefficient(crossSection_SRP, reflectivityCoeff)
solarRadiationPressure = SolarRadiationPressure(sun, R_e, spacecraftSRP)
numericalPropagator2.addForceModel(solarRadiationPressure)
print(crossSection_SRP)
initialDate = epochDate
t = [initialDate.shiftedBy(float(dt)) for dt in np.arange(0, duration, step_time)]
spacecraft1 = [numericalPropagator.propagate(tt) for tt in t]
spacecraft2 = [numericalPropagator2.propagate(tt) for tt in t]
sma = [x.getA() for x in spacecraft1]
sma2 = [x.getA() for x in spacecraft2]
diff_sma = np.array(sma2) - np.array(sma)
plt.plot(np.arange(0, duration, step_time),diff_sma)
plt.show()
What I get as a result, obtained from a 7 days propagation, is a very variable difference as can be seen in the figure below.
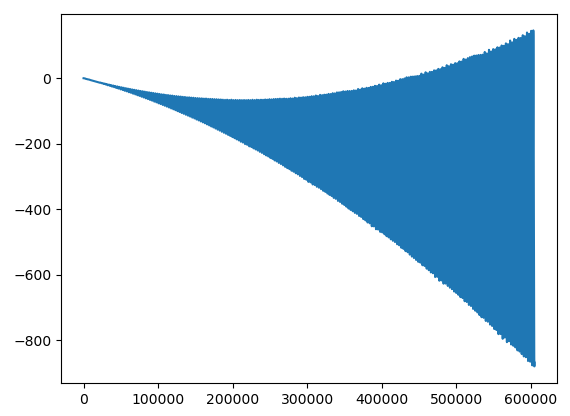
The trend is oscillating a lot, probably because from a numerical oscillator you get the osculating values. Should I take into account the average value of each period as the “mean” semi-major axis? Is this reasonable? I would not want the maneuver to happen when it is not needed…
Furthermore, a decay of around 400 meters seems really small after 7 days at around 480km altitude… is there any error in my code?