SSO behavior in numerical propagator

Orekit Python Wrapper usage
1

Hello,
I am relatively new to orekit. I am propagating a circular sun-synchronous orbit with a numerical propagator and Holmes-Featherstone Attraction Model using the Orekit Python Wrapper. Here is the important parts of my code :

#Circular orbit, initialized with Keplerian parameters

ra = 400 * 1000  # Apoapsis (km)
rp = 400 * 1000  # Periapsis (km)
inclination = radians(97.4)  
argument_of_perigee = radians(0.00)  
raan = radians(10.00)  
mean_anomaly = radians(0.00)  
semi_major_axis = (rp + ra + 2 * equatorial_earth_radius) / 2.0 
eccentricity = 1.0 - (rp + equatorial_earth_radius) / semi_major_axis  
epoch_orbital_parameters = simulation_start_datetime  

initial_kepler_orbit = KeplerianOrbit(
        semi_major_axis,  # semi-major axis in m
        eccentricity,  # eccentricity 0 to 1
        inclination,  # inclination rad
        argument_of_perigee,  # perigee argument rad
        raan,  # raan rad
        mean_anomaly,  # anomaly rad
        PositionAngleType.MEAN,  # type of anomaly -> MEAN
        EME2000_frame,  # parameter frame
        epoch_orbital_parameters,  # date of orbital parameters
        mu_m3_s2,  # mu m^3/s^2
    )
#Integrator

integrator = DormandPrince853Integrator(
        step_size / 10,  # minimum time step
        step_size,  # maximum time step
        1.0e-10,  # relative tolerance
        1.0e-10,  # absolute tolerance
    )

#define propagator
propagator = NumericalPropagator(integrator)
propagator.setOrbitType(OrbitType.CIRCULAR)

#add gravity model
gravity_field = GravityFieldFactory.getNormalizedProvider(70, 70)
gravity_model = HolmesFeatherstoneAttractionModel(itrf_frame, gravity_field)

propagator.addForceModel(gravity_model)

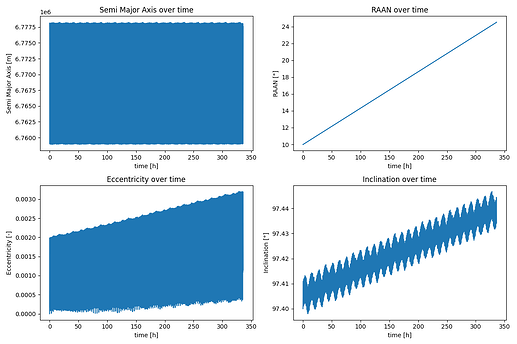
When I propagate for a time span of two weeks, I get these results for a few orbital parameters:

orbit_output
orbit_output1200×800 68.7 KB

The RAAN and semi major axis behave as expected.
However, eccentricity and inclination increase in a linear way (apart from the oscillation), although I would expect them to stay constant. I am wondering wether the deviation is caused by a numerical error or if my code for the orbit definition is wrong.
Many thanks
Marvin

2

Hello @mpfl_ust ,

Those behaviors for eccentricity and inclination are also expected. The variations you see in eccentricity are due to the gravity field while what appears to be a linear evolution of the inclination is most likely due to the frame in which the orbital elements are computed (I assume you’re computing them in EME). If you compute them in TOD, the linear evolution should disappear. In fact, that is not a linear trend, but rather a part of a sine wave with a period of 1 year.

If you propagated the orbit for a full year you’ll see this:

image
image1920×1128 261 KB

In blue you have the evolution in EME (I used ICRF actually, but the two frames are very close) and in orange the same orbit rotated in TOD. As you can see the inclination is now constant. What you are seeing is the motion of the equator with respect to EME/ICRF

Best regards,
Emiliano

2 Likes