Repeating ground track does not repeat

Orekit Python Wrapper usage
1

Hello all,
I am currently trying to analyze different possibilities of orbits with repeating ground track. As a first step, I am using the method mentioned in https://arc.aiaa.org/doi/abs/10.2514/1.A32038?journalCode=jsr to obtain the semi-major axis (and altitude) based input eccentricity and inclination of the orbit. As an example, I obtain that for an eccentricity = 0.0 and inclination 97.0°, I obtain that I should have a repeating ground track for an orbit semi-major axis of 6938.013km (559.8764km altitude).

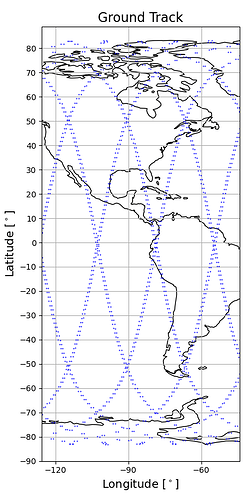
If I try to propagate such an orbit for more than 1 day though, I obtain that the resulting ground track is very close to the first cycle one, but not exactly aligned, as shown in the plot below.

image
image437×864 60.6 KB

I have attached below my current code for the numerical propagation and ground track generation: have I made some errors in the code? Do you obtain a repeating ground-track orbit with such parameters? I am currently only implementing a numerical propagator without any additional perturbation other than gravitational ones, therefore I would expect to see a matching ground-track…

year = 2026
month = 1
day = 1
hour = 6
minute = 0
seconds = 03.146
date_propagation = '2026-01-01T06:00:03.416'

J2 = -Constants.EIGEN5C_EARTH_C20

h = 559.8764
a = Constants.WGS84_EARTH_EQUATORIAL_RADIUS + h*1e3
e = 0.0
mu_e = Constants.EIGEN5C_EARTH_MU
R_e = Constants.WGS84_EARTH_EQUATORIAL_RADIUS
i = radians(97)
omega = radians(90.0)                                               # Orbit perigee argument [rad]
raan = radians(10.5)
true_anomaly = radians(0.0)                                        # Spacecraft true anomaly [rad]

inertialFrame = FramesFactory.getEME2000()

utc = TimeScalesFactory.getUTC()                                                  
epochDate = AbsoluteDate(year, month, day, hour, minute, seconds, utc)             
epoch = Time(date_propagation)                                                    

initialOrbit = KeplerianOrbit(a, e, i, omega, raan, true_anomaly,
                              PositionAngle.TRUE,
                              inertialFrame, epochDate, Constants.EIGEN5C_EARTH_MU)

period = initialOrbit.getKeplerianPeriod()

satellite_mass = 70. #37.                    # Spacecraft mass [kg]

duration =  2*60*60*24                                                # Propagation duration [s]
step_time = period/200                                                     # Propagation step-time [s]

# Numerical propagator definition
# Step size
minStep = 0.001
maxStep = step_time
initStep = step_time
positionTolerance = 1E-8
propagationType = OrbitType.CARTESIAN
tolerances = NumericalPropagator.tolerances(positionTolerance, initialOrbit, propagationType)
initialDate = epochDate
integrator = DormandPrince853Integrator(minStep, maxStep, orekit.JArray('double').cast_(tolerances[0]), orekit.JArray('double').cast_(tolerances[1]))
integrator.setInitialStepSize((initStep))

numericalPropagator = NumericalPropagator(integrator)
numericalPropagator.setOrbitType(propagationType)

# Generate ground track
ITRF = FramesFactory.getITRF(IERSConventions.IERS_2010, True)
earth = OneAxisEllipsoid(Constants.WGS84_EARTH_EQUATORIAL_RADIUS,
                         Constants.WGS84_EARTH_FLATTENING,
                         ITRF)

gravityProvider1 = GravityFieldFactory.getNormalizedProvider(20, 20)
numericalPropagator.addForceModel(HolmesFeatherstoneAttractionModel(earth.getBodyFrame(), gravityProvider1))
numericalPropagator.setInitialState(SpacecraftState(initialOrbit, satellite_mass))



t = [initialDate.shiftedBy(float(dt)) for dt in np.arange(0, duration, step_time)]

initialState = numericalPropagator.propagate(initialDate.shiftedBy(float(1E-10)))
numericalPropagator.setInitialState(initialState)
spacecraft1 = [numericalPropagator.propagate(tt) for tt in t]

pv = [x.getPVCoordinates() for x in spacecraft1]
p = [tpv.getPosition() for tpv in pv]

subpoint = [earth.transform(tp, inertialFrame, tt) for tt, tp in zip(t, p)]
lat = np.degrees([gp.getLatitude() for gp in subpoint])
lon = np.degrees([gp.getLongitude() for gp in subpoint])

# Create plot of ground track
ax = plt.axes(projection=crt.crs.PlateCarree())
ax.coastlines()
ax.plot(lon[1:-1], lat[1:-1], 'b.',markersize=1)
ax.plot(lon[0], lat[0], 'g.',markersize=10)
ax.plot(lon[-1], lat[-1], 'r.',markersize=10)
ax.set_title(r"Ground Track", fontsize=16)
ax.set_xlabel(r'Longitude $[\mathrm{^\circ}]$',fontsize=14)
ax.set_ylabel(r'Latitude $[\mathrm{^\circ}]$',fontsize=14)
plt.xlim(-180, 180)
plt.ylim(-90, 90)
plt.yticks([-90, -80, -70, -60, -50, -40, -30, -20, -10, 0, 10, 20, 30, 40, 50, 60, 70, 80, 90])
plt.xticks([-180, -150, -120, -90, -60, -30, 0, 30, 60, 90, 120, 150, 180])
ax.grid(True)
plt.show()
2

You can take a look at the Phasing tutorial for ideas. It is devoted to Sun Synchronous orbits with Earth phasing, which seems close to what you want.

3

Dear @luc , thank you for you help!
I was not looking at SSO with Earth phasing (just the latter only), but I was able to use part of the code devoted to Earth phasing correction in my code! The result I was obtaining from the theoretical model I mentioned in my opening post was about 4km away from the optimized semi-major axis from your code, which correctly generates a repeating ground track.

Why would that be the case though? In my numerical propagator I have only implemented the effect of gravitational harmonics (up to 20,20) and not have considered any other perturbations. The theoretical model accounts for J2 drift for RAAN, perigee argument and mean anomaly. Is that because the numerical propagator also takes into account higher order harmonics?

4

Yes, I guess the other harmonic terms are the culprit. For example J₃ does move eccentricity significantly if I remember well.

5

Hello @luc, sorry to bother you again. The results obtained with your tool have provided me with a repeating ground track for my initial orbit parameters, correcting the semi-major axis.

What I am trying to do now is to put several other satellites, spaced in true anomaly, on the same orbit. Which means that I am keeping all of the parameters obtained in the first case fixed, varying only the true anomaly of the others. What I obtain, though, is that only the first satellite maintains a repeating ground track orbit, while the other ground tracks start to drift! Is this supposed to happen?

I have tried to use the same tutorial you linked, inputting the same orbit but this time with a different initial true anomaly… and I have obtained a different semi-major axis!! Is this supposed to happen?

It seems like it is not possible to have multiple satellites on the same orbital plane, since only one can be set at the optimized semi-major axes while the others show a drift in the ground track… but this behaviour seems really unrealistic to me.

6

Yes. The osculating semi-major axis exhibits shot period terms, hence if you change the anomaly, you have to change the osculating semi-major axis.

Yes, same reason as above.

It is possible, but you need to change the tool slightly (if I remember well), because it works by looking at the ascending node only.

7

Dear @luc ,
thank you for your answer. So if I understood correctly everything is caused by the nature of osculating orbital elements (semi-major axis in particular). I have not understood well what your suggestion is regarding the modification to your tool, but I will explain how I intend to proceed.

What I will try to perform now is to initialize the orbit for the first satellite using keplerian elements and use the tool to obtain the corrected semi-major axis for this particular satellite, defined by an initial true anomaly. After this, instead of initializing the other propagators using the same orbital parameters and a delta_theta in true anomaly, I will go through the first orbit I propagated and extract the state of the first satellite when at the true anomaly of the other ones, and use these states for the initialization of the other propagators. In this way, I expect that each satellite will then follow the first “reference” orbit and show a repeating ground track behaviour.

My question then becomes: is this the right approach? How does one decide which is the reference orbit to follow? I am asking this since using your tool the altitude for a repeating ground track highly depends on the true anomaly, as you have explained, therefore it seems like that choosing a different true anomaly for the initialization of the reference orbit will generate a different semi-major axis for the whole constellation. I would like to have a result that is not dependent on the true anomaly, but I am wondering whether it is possible or not due to the nature of osculating elements…

Is there a way to become independent of the true anomaly orbit initialization? Otherwise it would seem that my design would be working in reality if and only if all satellites have the correct initial state in the point in space defined by my reference orbit generated from my arbitrary true anomaly.

8

This should be close to the correct repeating orbit. There is one little glitch, though. When we optimize the parameters to find a repeating track, we take into account a lot of perturbations. Propagating the satellite until it is at the correct anomaly and then using this state but at the initial date changes the position of the satellite with respect to the perturbation (tesseral terms of the gravity field because Earth is not in the same orientation, and third body effects due to Sun and Moon). So this approach will work properly for says the zonal terms of the gravity field, which are the most important ones, but not for all perturbations. Hence you will not get a perfectly repeatable orbit.

Anyway, perfect repetition is never possible on the long term. What we do in the tool is find an initial orbit that is good for one cycle, but then as perturbations will happen, on the long term users must do some station keeping to remain close to repetition ground track, so the output of the tool is just a good initial state.

I have checked the input parameters of the tool. In fact you can use it for finding the proper orbit for each satellite independently. It does not always compute the repetition at ascending node as I suggested in a previous post, but it has a referenceLatitude and a referenceAscending parameters. So if you compute the repetition for one satellite at zero latitude and ascending but for another satellite use for example +60° latitude and ascending, then you should get something close to what you need.

9

Dear @luc ,
thank you so much for the insights you have given me on the topic.
I have one final question though: while using your tool, which correctly adapts the height of the semi-major axis depending on the repeating ground track cycle to follow, I am able to find an orbit that repeats its ground track after the number of orbits used as input.

What is different though, is that the number of days required for the ground track to repeat do not match anymore! What happens is that if I set the propagator to run up to the final step “NbOrbits * period”, the spacecraft ground track will almost perfectly match. If I set the same value to “NbDays * 24 * 60 * 60”, what happens is that the spacecrafts propagates for a bit more (in some cases more than one orbit!) while still following a repeating ground track from the Nbth orbit.
The repeating ground track will still be maintained of course, but since the spacecraft “continues” along its trajectory it looks like the ground track repeats a bit earlier than the NbDays I set, since the semi-major axis found with your tool is slightly lower than my first guess. As I said, when I set the propagation end step using the initial number of orbits, the two points almost perfectly match.

Is this supposed to happen? Or should it be possible to correctly tune both the number of days and number of orbits per repeat cycle?

10

As you mentioned earlier that you are not using a Sun Synchronous Orbit, so the relative rotation of Earth with respect to orbital plane is not 24 hours. So the number of “days” should not be interpreted with solar mean days (i.e. 24 hours) in mind, but rather as “number of Earth rotations with respect to orbital plane drift due to J₂”.

1 Like
11

Dear @luc you are right! The correct way to estimate the repeat cycle is considering the nodal day, which for a non-SSO orbit does not correspond to a solar day.

I have one last question though: the non-repeating issue was caused by the fact that the propagator initialized the orbit with the semi-major axis that I obtained from theory. Once I have used your tool, I managed to adjust the semi-major axis in a way to have a repeating ground track… and I have noticed that the average semi-major axis along one orbit actually matched the one from theory!

So everything was caused by the fact that I was initializing the propagator with orbital parameters that are actually “averaged” while I should have used the semi-major axis that “locally” would have brought the satellite to an orbit (with repeating ground track) having the average semi-major axis I used as an input.

My question is: after these considerations, is there no easy way to propagate a set of satellites on the same orbit having the same semi-major axis? Because what I got from this problem is that the “local” semi-major axis needed to initialize the same orbit differs depending on the initial true anomaly, therefore only adding a delta_theta would not propagate the same trajectory for each satellite, correct? At least I was not getting repeating ground tracks for my other satellites in this way.

In my case, I had to either re-generate the semi-major axis for each satellite, or either propagate the first satellite and then initialize each other satellite based on the state of the first one in my target true anomalies… but in general, how does one ensure that the satellites are actually following on the same orbit if a shift in the initial state true anomaly might bring differences?

12

I guess this could be done using mean elements rather than osculating elements. However, if we optimize the orbits finely using numerical propagator, it uses works in osculating parameters only. Working with mean parameters involve using a different propagator, like DSST for example.

13

Dear @luc , thank you for the insight. I wanted to ask you one last thing:
I was able to generate my full set of satellites with different phasing and planes, and what resulted from your tool was that, due to osculating elements, each had to be initialized with a different semi-major axis.

What I am looking for is a way to make sure, once I initialize my satellite and use the functions I need in my tool, that the propagation of each spacecrafts ends when its ground track starts repeating itself. As you can see from my first post, I am propagating shifting by a dt, that I have set to be the orbital period of the orbit, evaluated as the Keplerian period from the osculating semi.major axis.

I need to have access to two things:

  • the penultimate SpacecraftState() before the ground track repeats
  • the exact instant in time, which most likely will not be a multiple of dt, at which the spacecraft starts repeating its ground track.

My initial idea was to set a check on the latitude/longitude and z-axis velocity, but what happens for some satellites is that sometimes the dt makes it such that the penultimate step is slightly earlier than the first one… so that the next one (the first of the new orbital cycle) ends up a bit further away from the first one, even though if one joins the two with a line it is clear that the ground track is repeating… but this skips the check.

Is it possible to obtain what I need? I see two ways of doing this:

  • define a dt for every satellite (which is initialized with a different semi-major axis) in such a way that the ground track not only repeats itself, but the first projections of the first and second cycle are really close to each other for all satellites.
  • propagate each satellite with a fixed dt, and exit the propagation when the ground track starts repeating, obtaining information on the penultimate step before the repetition, and the time-stamp at which the ground track starts repeating. Since I approximately know the repetition duration (multiple of nodal days), I could put a check from a few steps earlier.
14

Maybe you could use a LatitudeCrossingDetector and a counter to stop each propagation exactly at the n-th crossing of the initial latitude.