Propagation of GRAIL-A

[Rafa]

I have recently been trying to reproduce GRAIL-A’s trajectory as accurately as possible. To that extent, I was first looking for a source of state vectors as accurate as possible. I asked about this a while ago on SE exchange, and from the replies I got, it seems the best option would be the SPK kernels from here.

So I used my previous implementation in Orekit of SPK readers (see this MR) to read the SPK kernels for the 3rd-11th of April 2012. As far as I have read, this was a period where there was no manoeuvres, so it should make an easier starting point.

As a side note, I have verified that the results obtained when reading SPK kernels with my java implementation match exactly those obtained with CSPICE and with another previous implementation in R by myself, so the extracted reference positions and velocities should be correct.

From reading the kernels as well, it can be seen that the provided reference state vectors are in a frame of class 1 with a central body with NAIF code 301. So the state vectors are given in ICRF centered in the Moon.

So for a first test, I have tried to set up a numerical propagator considering only Moon spherical harmonics. I am currently using the
GRGM1200B model.

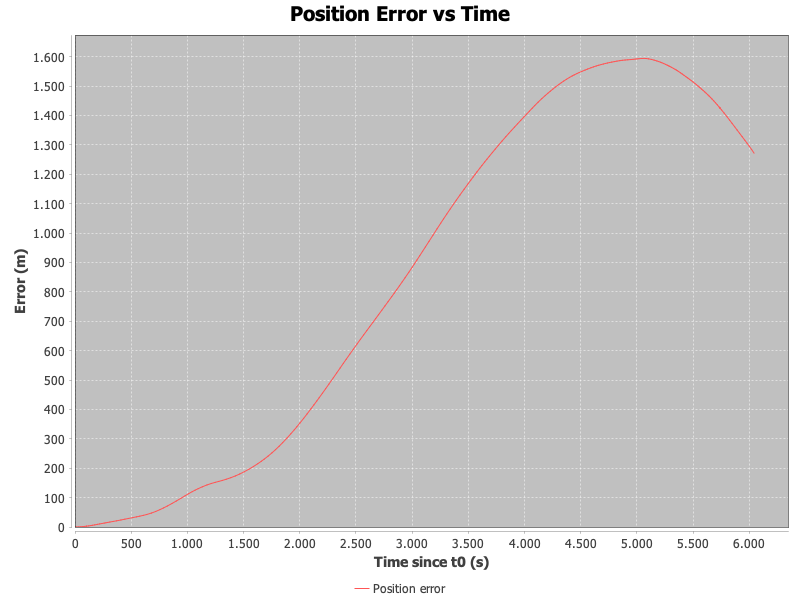
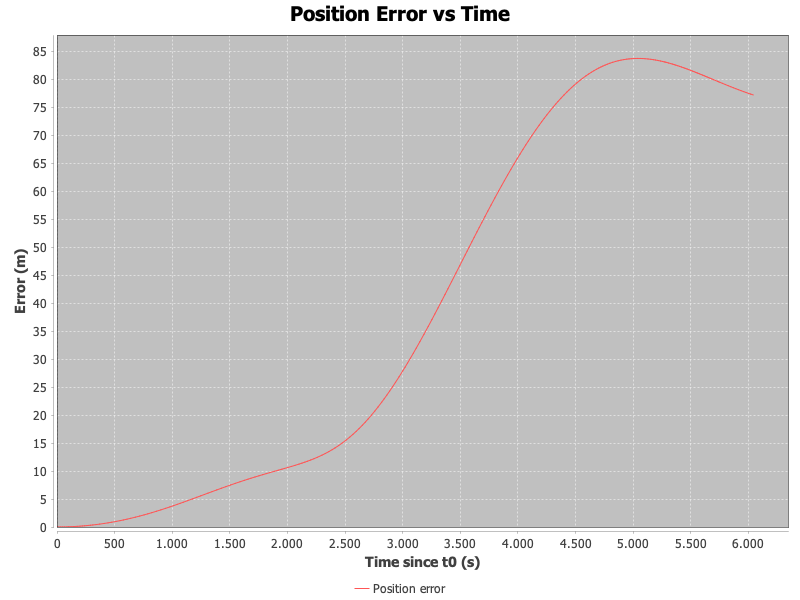
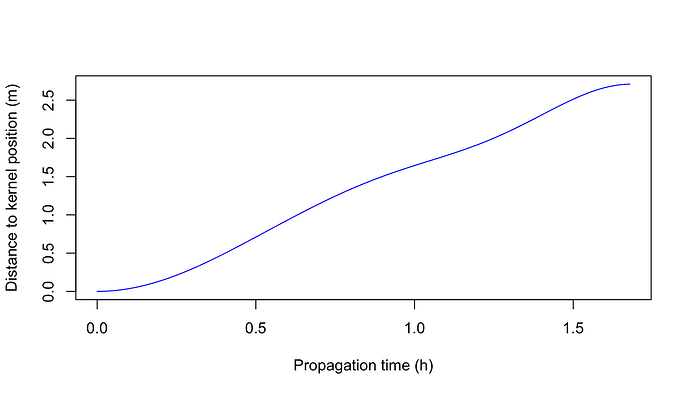
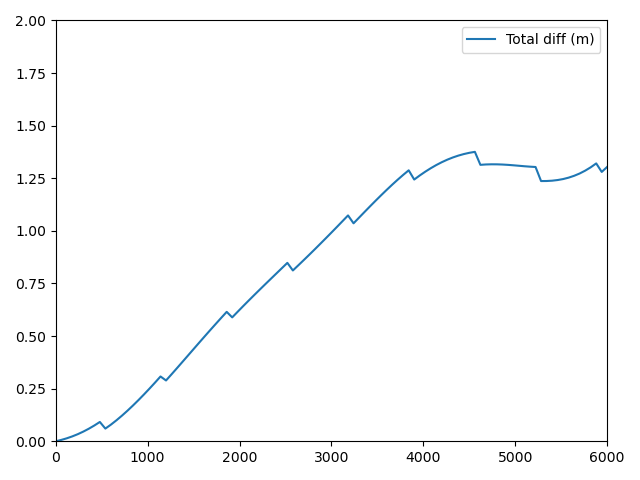
Using up to degree and order of 350 and propagating for a bit less than 2 hours, I get a final position error of over 1200 m, which seems too high to me. I have also done a plot of the position error versus time (using as propagation targets the epochs of each extracted reference state vector), and get the attached.

I have also attached my current attempt at setting this up. When setting up the SPH force model for the Moon, I’ve given the inertial frame centered on the Moon as the frame for the HolmesFeatherstoneAttractionModel as suggested in this answer. From the documentation here it says to use a rotating frame though, so just in case I also tried the default non-inertial frame centered on the Moon, but that didn’t help either.

The propagation error is too high I’d say, and I feel like I’m missing something very basic here! So any insights would be very appreciated

Thanks a lot!

App.java (8.1 KB)

[DDega]

Hi @Rafa,
sorry if I did not update you on the results from your implementation of the reader of the SPK kernels, unfortunatively I got quite busy with LEOP activities.
I can confirm you that when comparing the results from the propagation between Orekit and GMAT (using the native implementation of the SPK Kernels) the two are quite well aligned.
I set up the HolmesFeatherstoneAttarctionModel with the moonPA reference frame, which is constructed starting from the precise pole position and principal axis orientation obtained with your readers ( see our old discussion Updates for High Fidelity Heliocentric Propagation - #36 by Rafa) .
Here after an example code on how I have defined the moonPA reference frame.

First I define the position of the Frame (which I am sure I have used a way too complicated method)

public class LME2000PositionProvider implements TransformProvider{
    Frame ref; 
    
    public LME2000PositionProvider(Frame ref){
        this.ref = ref; 
    }
    @Override
    public Transform getTransform(AbsoluteDate date) {
        final Vector3D translation11 = CelestialBodyFactory.getMoon().getPVCoordinates(date,ref).getPosition().negate();
        final Vector3D velocity11 = CelestialBodyFactory.getMoon().getPVCoordinates(date,ref).getVelocity().negate();
        return new Transform(date,translation11,velocity11);
    }

    @Override
    public <T extends CalculusFieldElement<T>> FieldTransform<T> getTransform(FieldAbsoluteDate<T> date) {
        // Compute Field Translation 
        final FieldVector3D<T> translation = CelestialBodyFactory.getMoon().getPVCoordinates(date,ref).getPosition().negate();
        final FieldVector3D<T> velocity = CelestialBodyFactory.getMoon().getPVCoordinates(date,ref).getVelocity().negate();
        return new FieldTransform<>(date, translation, velocity);
    }

Then I define the Frame MoonPA as:

   public static Frame getMoonPA() {
       // Create a Moon-centered frame using the LME2000 position provider
       Frame moonCentered = new Frame(inertialFrame, new LME2000PositionProvider(inertialFrame), "moonCentered", true);
       
       // Define the MoonPA frame with a Moon Principal Axes (PA) rotation provider
       Frame MoonPA =  new Frame(moonCentered, new MoonPaRotationProvider(moonCentered), "MoonPA", true);
       
       return MoonPA; 
   }

The Rotation provider for now uses TabulatedProvided to define the orientation of the MoonPA ref frame wrt the ICRF frame.

[Rafa]

@DDega thanks a lot for this!
I see. So from what you describe, it seems the lunar SPH models have to be used together with the Moon PA frame. I’ve tried defining this frame as you suggested and the results have improved a lot, with now a position error of ~80 m after ~2 h propagation, see the plot below

However this still seems too high. I’ve tried adding solid Moon tides and Earth gravity as SPH, and none of those improved things.

However, when adding Earth attraction as a ThirdBodyAttraction, I get a bit of an improvement, see the next plot

So I wonder what went wrong when adding Earth gravity as another HolmesFeatherstoneAttractionModel?

I’m also wondering if there is still some error coming from some mistake in the definition of the Moon PA frame.

I’ve attached my updated implementation here (my attempt at adding Earth attraction as HolmesFeatherstoneAttractionModel is commented out).

Any insights greatly appreciated as always!

App.java (13.8 KB)

[DDega]

@Rafa great to see. I know that adding at least earth 2x2 or 2x0 harmonics for the Earth will help a lot and you might also add the cotribution of third body attraction of Jupiter and Venus (might not change a lot but it is quick to check).
Consider also that the SRP model for the GRAIL-A might be complicated to implement, try to add a simple SRP force model with the “Cannon Ball” approach.
In the meantime I will have a look at your code.

Davide

[Rafa]

@DDega thanks a lot! I’ve done some testing with my own asteRisk suit and checked what results I get when using just Moon SPH up to 350x350, with Earth just as a third body perturbation as well (no SPH), no SRP but including also third body perturbations from Sun, all other planets and Pluto. I get an error of ~2.5 m in the same propagation period. See the below plot

I’ve tried adding the same force models in Orekit, but the result looks almost exactly the same as in my previous attempt with just Moon SPH and Earth as third body perturbation. So I’m thinking there is still some sort of frame misalignment going on…

[DDega]

Could you try to define the MoonPA wrt the GCRF frame centered at the moon ? I don’t remember why I did not used the method CelestialBodyFactory.getMoon().getInertiallyOrientedFrame() but maybe there was a reason behind it.

[DDega]

@Rafa I have an update. I remember that the the method getInertiallyOrientedFrame() for the moon it gest a frame similar to the LME2000 (which is the mean equator mean equinox of the moon at the year 2000) while the file form NAIF specifically refers to the GCRF reference frame, so try to define a frame centered at the Moon like this:

public class LME2000PositionProvider implements TransformProvider{
    Frame ref; 
    
    public LME2000PositionProvider(Frame ref){
        this.ref = ref; 
    }
    @Override
    public Transform getTransform(AbsoluteDate date) {
        final Vector3D translation11 = CelestialBodyFactory.getMoon().getPVCoordinates(date,ref).getPosition().negate();
        final Vector3D velocity11 = CelestialBodyFactory.getMoon().getPVCoordinates(date,ref).getVelocity().negate();
        return new Transform(date,translation11,velocity11);
    }

    @Override
    public <T extends CalculusFieldElement<T>> FieldTransform<T> getTransform(FieldAbsoluteDate<T> date) {
        // Compute Field Translation 
        final FieldVector3D<T> translation = CelestialBodyFactory.getMoon().getPVCoordinates(date,ref).getPosition().negate();
        final FieldVector3D<T> velocity = CelestialBodyFactory.getMoon().getPVCoordinates(date,ref).getVelocity().negate();
        return new FieldTransform<>(date, translation, velocity);
    }

and then add the rotation obtained from the NAIF kernels.

[xzguo]

Hi, @Rafa , i am also very interested in how to setup a OREKIT propagator for moon’s satellite, and your previous propagation test of GRAIL-A really helps me.

here is my result, with moon’s SPH to 350x350, and earth+sun as third body perturbation, and no SRP. the reference orbit is taken from gralugf2012_094_2012_095.spk, and is from the started epoch 2012-04-03T00:00:00 to 6000s after.

But i have changed the MoonPA definition based on DE440 libration, which i believe is the best data i can get, and the transform is shown as,

phi, theta, psi = jplEph.getLibrations(jd)

rotation = Rotation(RotationOrder.ZXZ, RotationConvention.FRAME_TRANSFORM, phi, theta, psi)

actually, i have also defined the SCRF based on DE440 moon pos/vel.

there are jags in the curve, i have no idea why it happened. Maybe is bugs of my implementation of spk type 1 record reader.

[Danielepice99]

Hi @Rafa, I’m trying to perform a propagation using your classes for parsing the PCK files. I generate the MoonPA from LME2000 for the SPHmodel.

Do you know if there’s a way to reduce the size of the first PCKsegment (now, it covers about 1000 years)? I’d like to make the propagation faster, and providing less data might help.

[DDega]

Hi xzguo,

I am getting good results by using the implementation provided by @Rafa to compute the required rotation. My guess is that, with your implementation of the libration angle above, you are not interpolating between successive angles (or at least you are using a different interpolation method). That might explain the jumps you are seeing.

Thanks,
Davide

[xzguo]

hi, Davide @DDega .

Thanks for your suggestion. i am still trying to find out why there is such discontinuity. the libration angles are taken from python package jplephem. i am not sure what happens during its interpolation. i will check the transformation again.

BTW, could you share your choices of force model in the GRAIL-A propagator? And how is your current results compare to your previous?

thanks