Hi everyone,
I’m working on maximizing the precision of my Orekit propagator and have encountered an issue I’d like to get some insights on.
Background:
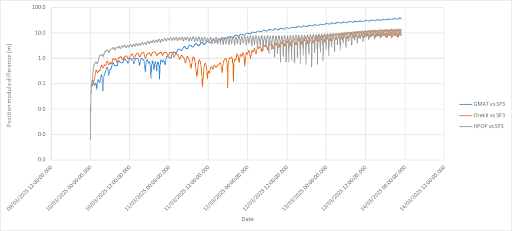
- Initially, my Orekit propagator showed excellent agreement with SP3 data for the Starlette satellite (a spherical satellite with photodiodes). The input parameters for Starlette (Cd=2, Cr=1.1, Cd_area=0.0452 m², Cr_area=0.0452 m², mass=47.29 kg) were derived specifically for that satellite. HPOP data also aligned well with the SP3 data, and comparisons between Orekit and HPOP for Starlette yielded similar results (see attached plots).
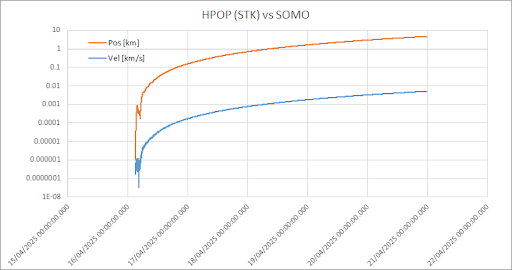
- However, when I changed the input parameters to values representative of other satellites (Cd=2.2, Cr=1.8, Cd_area=0.0025 m², Cr_area=0.0025 m², mass=2.455 kg), the agreement between Orekit and STK propagations significantly decreased, resulting in much larger errors (see attached plot).
Problem:
Intuitively, using the same input parameters in both Orekit and STK should produce comparable errors, right? The increased error with the new satellite parameters is puzzling. Is it possible that the spherical shape of Starlette, and consequently the accuracy of the drag model for Starlette, contributed to the initial high agreement? Could a less accurate drag model for non-spherical satellites be the source of the larger errors?
Request for Recommendations:
I’m aiming for the highest possible precision in my Orekit propagator. Any recommendations regarding force models, configuration settings, or general best practices would be greatly appreciated.
Plot comparing different propagators (like Orekit and STK/HPOP) and SP3 data
Plot comparing between Orekit and STK/HPOP changing input values from the above plot
(y-axis is in km sorry for that)
Orekit propagator setup
self.norad_id = norad_id
self.satellite_id = satellite_id
self.earth_mu = Constants.WGS84_EARTH_MU
self.sun_radius = Constants.SUN_RADIUS
self.sun_power = 3.846e26
self.four_pi = 4 * np.pi
self.mass = satellite_specifications.physical_properties["mass"]
self.eme2000_frame = FramesFactory.getEME2000()
self.itrf_frame = FramesFactory.getITRF(IERSConventions.IERS_2010, True)
self.sun = CelestialBodyFactory.getSun()
self.sun_frame = self.sun.getBodyOrientedFrame()
self.absolute_date_zero = AbsoluteDate()
self.earthRadius = Constants.WGS84_EARTH_EQUATORIAL_RADIUS
min_step = 1e-6
max_step = 100.0
init_step = 10.0
# Setup Earth and shapes
earthFlattening = Constants.WGS84_EARTH_FLATTENING
earthShape = OneAxisEllipsoid(self.earthRadius, earthFlattening, self.itrf_frame)
# Setup lighting model for irradiance calculations
self.lighting_model = ConicallyShadowedLightFluxModel(
self.sun_radius, self.sun, self.earthRadius
)
# Initialize integrator with optimal parameters for speed
integrator = DormandPrince853Integrator(min_step, max_step, 1e-15, 1e-15)
integrator.setInitialStepSize(init_step)
# Setup propagator
self.propagator = NumericalPropagator(integrator)
self.propagator.setOrbitType(OrbitType.CARTESIAN)
self.propagator.setMu(self.earth_mu)
# Add force models efficiently
# Gravity model
gravity_provider = GravityFieldFactory.getNormalizedProvider(70, 70)
gravity_model = HolmesFeatherstoneAttractionModel(self.itrf_frame, gravity_provider)
self.propagator.addForceModel(gravity_model)
# Atmospheric drag model
cssiSpaceWeatherData = CssiSpaceWeatherData("SpaceWeather-All-v1.2.txt")
atmosphere = NRLMSISE00(cssiSpaceWeatherData, self.sun, earthShape)
drag_area = satellite_specifications.physical_properties["reference_area"]
drag_coeff = satellite_specifications.physical_properties["drag_coefficient"]
dragSC = IsotropicDrag(drag_area, drag_coeff)
self.propagator.addForceModel(DragForce(atmosphere, dragSC))
# Solar radiation pressure model
srp_area = satellite_specifications.physical_properties["reference_area_radiation"]
srp_coeff = satellite_specifications.physical_properties["radiation_pressure_coefficient"]
isotropicRadiationSingleCoeff = IsotropicRadiationSingleCoefficient(srp_area, srp_coeff)
self.propagator.addForceModel(
SolarRadiationPressure(self.sun, earthShape, isotropicRadiationSingleCoeff)
)
# Third body perturbations
self.propagator.addForceModel(ThirdBodyAttraction(self.sun))
self.propagator.addForceModel(ThirdBodyAttraction(CelestialBodyFactory.getMoon()))