Orbit propagation - modified initial orbit?

nrol · September 14, 2018, 10:06am

Hi there,

I’m trying to propagate an cartesian orbit but I have a difference in the result when compared to STK for example. It seems that the initial orbit is modified by Orekit before propagation. It seems that the Numerical Integrator tolerance parameter is linked to this issue but I dont exactly understand how and why.

A good example of this problem is when I try to propagate a satellite, add a maneuver then propagate to another date. I then have 2 problems (probably linked) :

When I modify only the maneuver date, the propagated orbit changes (even the initial orbit) which is strange.
The initial orbit of the propagation after the maneuver is not same orbit as the last before the maneuver, even if the maneuver is null !

Here is the code I use for propagating the orbit and generating the OEM file. I may have done some modifications in the classes used for the OEM generation in order to have a proper CCSDS format.
ManoeuverPropagator.java (11.3 KB)

Any idea of what is happening and of what I can do to have a better propagation ?

Have a good day

edit : If you have ways to ooptimize the code, I’m open to suggestions

Christophe · September 17, 2018, 7:32am

Hello,

I didn’t look precisely at your problem but, in the provided code, you have 2 variables declared and named “vitesse”. I think your code should not compile.

For efficiency, you could use a stepHandler for the ephemeris output.
Or, if you want to keep your loop, set your propagator to EPHEMERIS_MODE, after propagation get the BoundedPropagator which is the result of the propagation and use it in your loop (example below for this 2nd method).

With your method, your re-propagate each time and it’s time-consuming.

		/* ======================= PROPAGATION JUSQU'A LA MANOEUVRE ======================= */
		propagator.setEphemerisMode();
		// Extrapolation de la date initiale à la date de la manoeuvre
		SpacecraftState beforeManeuverState = propagator.propagate(dateManeuvre);

		BoundedPropagator boundedProp = propagator.getGeneratedEphemeris();
		
		// Affichage de l'orbite avant manoeuvre
		System.out.println(" Orbite avant manoeuvre :");
		System.out.println("  Date de la manoeuvre : " + beforeManeuverState.getDate());
		System.out.println("  " + beforeManeuverState.getOrbit());

		// Paramètres de l'éphéméride
		final double propagationDurationSeconds = dateManeuvre.durationFrom(dateDebut);

		// Initialisation de la liste des états à enregistrer
		List<SpacecraftState> states = new ArrayList<SpacecraftState>();

		// Enregistrement des états
		for (double dt = 0.0; dt <= propagationDurationSeconds; dt += stepSizeSeconds) {
			states.add(boundedProp.propagate(dateDebut.shiftedBy(dt)));
		}

Christophe

Christophe · September 17, 2018, 8:06am

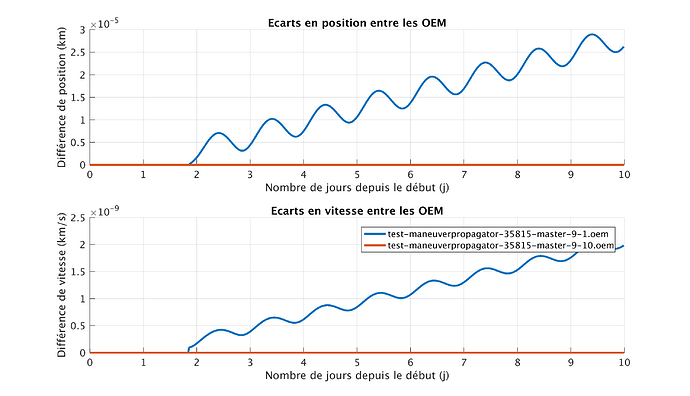
I ran your code. I didn’t observe the problem of modification of the orbit.
But I have a question: the date of the maneuver is the same as the date for the end of the propagation. So, you do not propagate after the maneuver: that’s what you want to do?

Orbite initiale :
Date de debut : 2018-08-31T00:00:00.000
Cartesian parameters: {2018-08-31T00:00:00.000, P(3.77279251691374E7, 1.8861471230199E7, -26502.8594459892), V(-1372.8424195657, 2750.00801092554, 0.04512254183365766), A(-0.20039231735928986, -0.10018292582166853, 1.4077024901899075E-4)}
Orbite avant manoeuvre :
Date de la manoeuvre : 2018-09-10T00:00:00.000
Cartesian parameters: {2018-09-10T00:00:00.000, P(3.39637460890208E7, 2.5014699658136625E7, -43029.03891703195), V(-1821.222271099359, 2475.7268093313883, 0.6779890964996327), A(-0.18037992560927552, -0.13286191386885463, 2.2722305049791065E-4)}
dV : {-0; 0; 0}
Orbite après manoeuvre :
Date de la manoeuvre : 2018-09-10T00:00:00.000
Cartesian parameters: {2018-09-10T00:00:00.000, P(3.39637460890208E7, 2.5014699658136625E7, -43029.03891703195), V(-1821.222271099359, 2475.7268093313883, 0.6779890964996327), A(-0.1803804399785667, -0.1328523219564699, 2.285259391400916E-4)}
Orbite finale :
Date de fin : 2018-09-10T00:00:00.000
Cartesian parameters: {2018-09-10T00:00:00.000, P(3.39637460890208E7, 2.5014699658136625E7, -43029.03891703195), V(-1821.222271099359, 2475.7268093313883, 0.6779890964996327), A(-0.1803804399785667, -0.1328523219564699, 2.285259391400916E-4)}

With another date for the maneuver (1 day before) and a deltaV of 0m/s :

Orbite initiale :
Date de debut : 2018-08-31T00:00:00.000
Cartesian parameters: {2018-08-31T00:00:00.000, P(3.77279251691374E7, 1.8861471230199E7, -26502.8594459892), V(-1372.8424195657, 2750.00801092554, 0.04512254183365766), A(-0.20039231735928986, -0.10018292582166853, 1.4077024901899075E-4)}
Orbite avant manoeuvre :
Date de la manoeuvre : 2018-09-09T00:00:00.000
Cartesian parameters: {2018-09-09T00:00:00.000, P(3.438932101021747E7, 2.442717536324472E7, -41980.147241723505), V(-1778.3170966640075, 2506.663228015379, 0.6940894145664359), A(-0.18263615645183995, -0.12973846422836352, 2.2127683011649964E-4)}
dV : {-0; 0; 0}
Orbite après manoeuvre :
Date de la manoeuvre : 2018-09-09T00:00:00.000
Cartesian parameters: {2018-09-09T00:00:00.000, P(3.438932101021747E7, 2.442717536324472E7, -41980.147241723505), V(-1778.3170966640075, 2506.663228015379, 0.6940894145664359), A(-0.1826343492059699, -0.12972751843750605, 2.2294760832250815E-4)}
Orbite finale :
Date de fin : 2018-09-10T00:00:00.000
Cartesian parameters: {2018-09-10T00:00:00.000, P(3.396374608907751E7, 2.5014699658131048E7, -43029.03892086521), V(-1821.2222710931653, 2475.7268093321964, 0.6779890962555428), A(-0.18037992560903324, -0.13286191386842472, 2.27223050517581E-4)}

With a deltaV of 1m/s:

Orbite initiale :
Date de debut : 2018-08-31T00:00:00.000
Cartesian parameters: {2018-08-31T00:00:00.000, P(3.77279251691374E7, 1.8861471230199E7, -26502.8594459892), V(-1372.8424195657, 2750.00801092554, 0.04512254183365766), A(-0.20039231735928986, -0.10018292582166853, 1.4077024901899075E-4)}
Orbite avant manoeuvre :
Date de la manoeuvre : 2018-09-09T00:00:00.000
Cartesian parameters: {2018-09-09T00:00:00.000, P(3.438932101021747E7, 2.442717536324472E7, -41980.147241723505), V(-1778.3170966640075, 2506.663228015379, 0.6940894145664359), A(-0.18263615645183995, -0.12973846422836352, 2.2127683011649964E-4)}
dV : {-0,5786160259; 0,8156000513; 0,0002258378}
Orbite après manoeuvre :
Date de la manoeuvre : 2018-09-09T00:00:00.000
Cartesian parameters: {2018-09-09T00:00:00.000, P(3.438932101021747E7, 2.442717536324472E7, -41980.147241723505), V(-1778.895712689876, 2507.478828066633, 0.694315252387715), A(-0.1826343492059699, -0.12972751843750605, 2.2294760832250815E-4)}
Orbite finale :
Date de fin : 2018-09-10T00:00:00.000
Cartesian parameters: {2018-09-10T00:00:00.000, P(3.411623024064095E7, 2.4806046645751208E7, -43087.63729792053), V(-1806.5917041274254, 2487.675070421675, 0.6589003484971477), A(-0.18119191106486746, -0.13175527530648762, 2.275305337229292E-4)}

One remark: for the computation of the deltaV, you could code it:

		Vector3D dVVector = vitesse.normalize().scalarMultiply(dVValue);

instead of

		Vector3D dVVector = new Vector3D(dVValue * vitesse.getX() / vitesse.getNorm(),
				dVValue * vitesse.getY() / vitesse.getNorm(),
				dVValue * vitesse.getZ() / vitesse.getNorm());

Christophe

nrol · September 17, 2018, 9:28am

Thank you for your answers.

I took your remarks into consideration and modified the vitesse variable, the dVVector computation and added the ephemeris mode (I thought I used it but apparently forgot half the usefull lines of code…). I’ll try with the stepHandler on a second version. For that future version, the propagation mode should be “Master mode” as described on that page ?

With the ephemeris propagation correctly implemented, the propagated orbit seems to be much better!

Even in the orbits you showed, there is however still a small diffference between the two cases at dv=0m/s with two different dates. The difference is very small (<1mm) but if you know where it could come from, I’d be very interested.
Do you have any idea about that ?

Nicolas

Christophe · September 17, 2018, 1:53pm

Ok, I didn’t understand that you talked about the acceleration.

When you rebuild the orbit after the maneuver, after the declaration of the cartesianOrbit, the acceleration is computed only with the central force.
But the acceleration just before the maneuver is the acceleration computed during the propagation, so with the full models of perturbations. That’s why the accelerations are different.

If you display the state after maneuver from the boundedPropagator of the 2nd propagation (after the maneuver), they should be identical.
ie: boundedProp.propagate(boundedProp.getMinDate());

Christophe

nrol · September 17, 2018, 3:48pm

Well I didn’t understand it either but seeing the values of the acceleration, it may be the reason of the observable differences.

There is however still a small difference between a maneuver the 01/09 and one the 10/09:

Here is an updated version of the code :
ManeuverPropagation_mastermode.java (11.4 KB)

With a maneuver of 0m/s the 01/09/2018 at 01h00, the console output is the following :

Orbite initiale :
Date de début : 2018-08-31T00:00:00.000
Cartesian parameters: {2018-08-31T00:00:00.000, P(3.77279251691374E7, 1.8861471230199E7, -26502.8594459892), V(-1372.8424195657, 2750.00801092554, 0.04512254183365766), A(-0.20039105190141654, -0.10018444972438904, 1.4169550626880686E-4)}
Orbite en fin de propagation :
Date de fin : 2018-09-01T01:00:00.000
Cartesian parameters: {2018-09-01T01:00:00.000, P(3.10710382907986E7, 2.8535097918909054E7, -25533.85799639652), V(-2077.6794344539444, 2264.4437171303443, 0.6330152605735903), A(-0.16496233177155464, -0.15150153045018774, 1.3772286843900033E-4)}
dV : {-0; 0; 0}
Orbite après manoeuvre :
Date de la manoeuvre : 2018-09-01T01:00:00.000
Cartesian parameters: {2018-09-01T01:00:00.000, P(3.10710382907986E7, 2.8535097918909054E7, -25533.85799639652), V(-2077.6794344539444, 2264.4437171303443, 0.6330152605735903), A(-0.16496328350926823, -0.1514993932261263, 1.35565120686435E-4)}
Orbite initiale :
Date de début : 2018-09-01T01:00:00.000
Cartesian parameters: {2018-09-01T01:00:00.000, P(3.10710382907986E7, 2.8535097918909054E7, -25533.85799639652), V(-2077.6794344539444, 2264.4437171303443, 0.6330152605735903), A(-0.16496233177155462, -0.15150153045018772, 1.377228684390003E-4)}
Orbite en fin de propagation :
Date de fin : 2018-09-10T00:00:00.000
Cartesian parameters: {2018-09-10T00:00:00.000, P(3.396374607230927E7, 2.5014699678586394E7, -43029.03873951323), V(-1821.2222727507792, 2475.7268082216992, 0.6779891048675524), A(-0.18037992553756985, -0.13286191399002403, 2.2722304957728922E-4)}
Orbite finale :
Date de fin : 2018-09-10T00:00:00.000
Cartesian parameters: {2018-09-10T00:00:00.000, P(3.396374607230927E7, 2.5014699678586394E7, -43029.03873951323), V(-1821.2222727507792, 2475.7268082216992, 0.6779891048675524), A(-0.18037992553756982, -0.13286191399002403, 2.272230495772892E-4)}

With a maneuver at the end of the propagation, the output is the following :

Orbite initiale :
Date de début : 2018-08-31T00:00:00.000
Cartesian parameters: {2018-08-31T00:00:00.000, P(3.77279251691374E7, 1.8861471230199E7, -26502.8594459892), V(-1372.8424195657, 2750.00801092554, 0.04512254183365766), A(-0.20039105190141654, -0.10018444972438904, 1.4169550626880686E-4)}
Orbite en fin de propagation :
Date de fin : 2018-09-10T00:00:00.000
Cartesian parameters: {2018-09-10T00:00:00.000, P(3.39637460890208E7, 2.5014699658136625E7, -43029.03891703195), V(-1821.222271099359, 2475.7268093313883, 0.6779890964996327), A(-0.18037992560927554, -0.13286191386885463, 2.2722305049791068E-4)}
dV : {-0; 0; 0}
Orbite après manoeuvre :
Date de la manoeuvre : 2018-09-10T00:00:00.000
Cartesian parameters: {2018-09-10T00:00:00.000, P(3.39637460890208E7, 2.5014699658136625E7, -43029.03891703195), V(-1821.222271099359, 2475.7268093313883, 0.6779890964996327), A(-0.1803804399785667, -0.1328523219564699, 2.285259391400916E-4)}
Orbite finale :
Date de fin : 2018-09-10T00:00:00.000
Cartesian parameters: {2018-09-10T00:00:00.000, P(3.39637460890208E7, 2.5014699658136625E7, -43029.03891703195), V(-1821.222271099359, 2475.7268093313883, 0.6779890964996327), A(-0.1803804399785667, -0.1328523219564699, 2.285259391400916E-4)}

Any idea of where this difference comes from ? Is it from the infinitesimal difference seen at the maneuver on the 01/09 ? If so, would it be possible not to have this difference ?

Thanks for your answers

Nicolas

evan.ward · September 17, 2018, 4:56pm

Hi Nicolas,

Stopping to insert maneuvers introduces three types of errors in numerical propagation. These errors can be reduced by careful programming, but not eliminated entirely.

First is numerical noise due to transforming back and forth from the states the ODE integrator uses to the SpacecraftState values that the application uses. Each transformation back and forth can introduce many ulps of error. Reduce this error by performing computations in the same orbit type and frame as the propagator.

Second is interpolation error in the SpacecraftStates computed by the propagator. Any time you request the state of the spacecraft, other than at an ODE integrator step boundary, it is interpolated from the integrator steps near by. Reduce this error by using states at integrator steps. Force the integrator steps to be when you want them by using a fixed step integrator. Determine if a state is interpolated or not by using setEphemerisMode(OrekitStepHandler) or setMasterMode(OSH) and then calling isCurrentStateInterpolated() on the OrekitStepInterpolator.

Third is error due to different series of integrator steps being chosen. If propagation is reset at an interpolated state then it starts a new series of steps. When propagation is restarted the integrator is reinitialized and, if it is an adaptive step size integrator, a new series of steps is chosen. Reduce by using a fixed step integrator so you can control when the force model is evaluated.

Good news is the last two error are probably what you are seeing and these are both controlled by the tolerance parameter. Since the errors you are seeing are less than the requested tolerance it seems that everything is working as expected. Keep in mind that the errors will grow over time (and the growth will accelerate) due to the dynamics of the system so eventually the error tolerance will be exceeded.

Regards,
Evan

nrol · September 20, 2018, 1:00pm

Thank you for your precise answer !

In order to change from an adaptative step to a fixed step, I’ll have to change the integrator used, right ?
Which one would you use in my case, in order to keep a good precision ?

Have a good day
Nicolas

pascal.parraud · September 20, 2018, 2:53pm

Hi Nicolas,

The step of the handler is independent from the step of the integrator, so you can use a fixed step handler with an adaptive step size integrator.

But if you want a fixed step integrator, according to Evan’s analysis, you should use at least a 4th order RK integrator, such as the ClassicalRungeKuttaIntegrator or the GillIntegrator, or the LutherIntegrator, a 6th order RK integrator.

Regards,

Pascal