Orbit Determination and Covariance ellipsoid

Orekit Python Wrapper usage
1

Hi everyone!

I am working in obtaining the ellipsoid of covariance to know with a certain probability where my spacecraft is going to be. Following the tutorial of @yzokras:

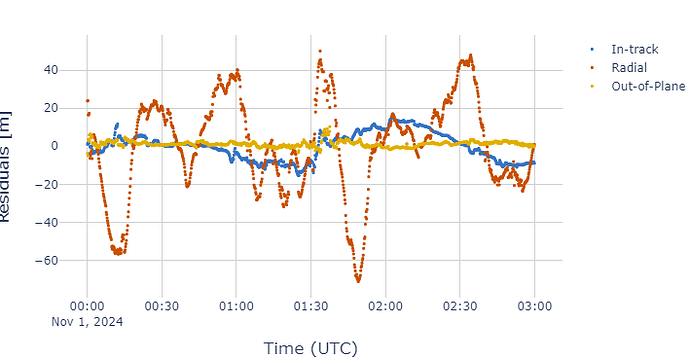
From a set of GPS data of my satellite, I perform OD with BLS, obtaining the following residuals in orbital frame:

imagen
imagen709×369 34.1 KB

(I estimated the CD parameter, I included third body forces and harmonic coefficients up to 64)

Propagating the covariance with the estimated propagator I obtain the following standard deviations at each timestamp:

imagen
imagen749×358 20.7 KB

I know that the magnitude of the standard deviations obtained depends directly on the sigma of my GPS I use at the beginning of my estimation procedure, so:

  1. How can I get real values of these standard devilations that match with my residuals, to know the real ellipsoid at any time? (I want my 3sigma to be more than my residuals amplitude if that makes sense)

  2. When I compute the covariance matrix in orbital frame, I saw that at some timestamps some elements of the diagonal are negative, do you know why this could be happening?

  3. Looking at my residuals, do you know why I have much more in the radial component? I could reduce the out of plane component adding third body perturbations and the along track component estimating the CD.

Thank you so much,
Checa

2

When you’re interpreting the covariance from the BLS algorithm (and to an extent the EKF and UKF) you need to keep in mind that it is computed using the theoretical measurement std, not the actual residuals.

That means an important step is understanding the errors in your measurements. When you plot your residuals it’s really helpful to plot normalised residuals (normalised by the noise std). The normalised residuals should have zero mean and unit standard deviation. If the std. dev. is larger, or smaller than 1, then you can adjust your measurement noise until the normalised residuals are roughly zero-mean. Resolving a non-zero mean is a bit more complicated (e.g. measurement biases, environmental effects on the measurements or even the choice of force models).

Also, remember that the covariance represents the expected estimation error on average. You should expect your calculated residuals to roughly follow the shape of the evolution of the covariance over time, but not exactly.