Hi,
I having issue to compute correctly the mean/true solar time for our project.
We want the users to define the ascending node with a mean or true solar time.
Here is the code we used to compute our values :
from math import *
from orekit.pyhelpers import setup_orekit_curdir
from org.orekit.bodies import CelestialBodyFactory
from org.orekit.utils import PVCoordinatesProvider
from org.orekit.time import AbsoluteDate, TimeScalesFactory
from org.orekit.frames import FramesFactory
from org.orekit.utils import Constants, IERSConventions
from org.hipparchus.util import FastMath, MathUtils
from org.orekit.orbits import KeplerianOrbit, PositionAngle
from org.orekit.data import DataContext
from org.orekit.bodies import GeodeticPoint
from org.orekit.bodies import OneAxisEllipsoid
vm = orekit.initVM()
setup_orekit_curdir('/data/OREKIT-DATA')
conventions = IERSConventions.IERS_2010;
gmst = conventions.getGMSTFunction(TimeScalesFactory.getUT1(conventions, False));
# Return the inertial frame used aka Veis1950
def getInertiallyOrientedFrame():
return FramesFactory.getVeis1950()
# Convert the julian day from FIFTIES_EPOCH to AbsoluteDate
def julianToAbsoluteDate(julianDay):
return AbsoluteDate(AbsoluteDate.FIFTIES_EPOCH, julianDay*Constants.JULIAN_DAY, TimeScalesFactory.getTT())
# Get the rotation angle between inertial frame and rotational frame for the Earth at the given date
def getPrimeMeridianAngle(julianDate):
earth = CelestialBodyFactory.getEarth()
date = julianToAbsoluteDate(julianDate)
referenceFrame = getInertiallyOrientedFrame()
rotationalFrame = earth.getBodyOrientedFrame()
transform = referenceFrame.getTransformTo(rotationalFrame,julianToAbsoluteDate(julianDate))
angle = transform.getRotation().getAngle()
# angle rotation is defined around 0 and PI. As we want the result between -PI and PI
# we have to check the sign of rotation axis ( Vector3D.PLUS_K or Vector3D.MINUS_K)
if transform.getRotation().getAxis(RotationConvention.FRAME_TRANSFORM).getZ() < 0.:
angle = -angle
return angle
# Convert the longitude in earth body oriented frame
def computeRotationalLongitude(longitude, julianDate):
return longitude - getPrimeMeridianAngle(julianDate)
# Return the sub solar point in the earth's rotational reference frame
def getSubSolarPoint(julianDate):
earth = CelestialBodyFactory.getEarth()
sun = CelestialBodyFactory.getSun()
date = julianToAbsoluteDate(julianDate)
# Get sun position in earth body oriented frame
sunPVProvider = PVCoordinatesProvider.cast_(sun)
sunPosition = sunPVProvider.getPVCoordinates(date, earth.getBodyOrientedFrame()).getPosition()
# Convert cartesian coordinates to lat/long/altitude
earthEllipsoid = OneAxisEllipsoid(Constants.IERS2010_EARTH_EQUATORIAL_RADIUS, Constants.IERS2010_EARTH_FLATTENING,
earth.getBodyOrientedFrame())
return earthEllipsoid.transform(sunPosition, earth.getBodyOrientedFrame(), julianToAbsoluteDate(julianDate))
# Convert raan to true solar time
def raanToTrueSolarTime(inertialLongitude, julianDate):
rotationalLong = computeRotationalLongitude(inertialLongitude, julianDate)
sunLongitude = getSubSolarPoint(julianDate).getLongitude()
deltaLong = MathUtils.normalizeAngle(rotationalLong - sunLongitude, 0.) # Normalize between -π and +π
return 12.0 * (1.0 + deltaLong / FastMath.PI)
# Compute the mean solar time
def meanSolarTime(julianDay):
earth = CelestialBodyFactory.getEarth()
date = julianToAbsoluteDate(julianDay)
# compute angle between Sun and spacecraft in the equatorial plane
orbit = KeplerianOrbit(Constants.IERS2010_EARTH_EQUATORIAL_RADIUS,0.,0.,0.,0.,0.,PositionAngle.TRUE,getInertiallyOrientedFrame(),
date,earth.getGM())
position = orbit.getPVCoordinates().getPosition();
time = orbit.getDate().getComponents(TimeScalesFactory.getUTC()).getTime().getSecondsInUTCDay();
# The Greenwich Mean Sidereal Time is the hour angle between the meridian of Greenwich and mean equinox of date at 0h UT1
theta = gmst.value(date);
sunAlpha = theta + FastMath.PI * (1 - time / (Constants.JULIAN_DAY * 0.5))
dAlpha = MathUtils.normalizeAngle(position.getAlpha() - sunAlpha, 0.0) # Normalize between -π and +π
# convert the angle to solar time
return 12.0 * (1.0 + dAlpha / FastMath.PI);
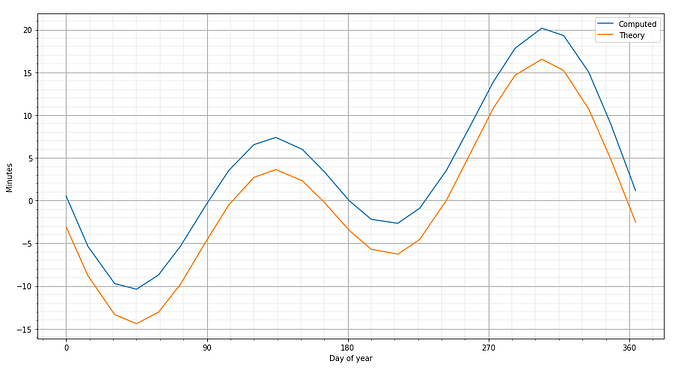
Then each 15 days, I compute the difference bewteen mean solar time and true solar time, and display the resulting curve over the equation of time.
I have a shift close to 3min44 from the computed values to the theorical one which I cannot explain.
Anyone ?
Regards,