Mean anomaly in time, keplerian propagation

Orekit Python Wrapper usage
1

Hello orekit community,

I just created a function to propagate with the keplerian propagator knowing an initial conditon E0, a initial time, a final time and the inertialFrame. Where E0 = [a,e,i,pa,raan,M], the keplerian orbital parameters.

Here is the function I designed :

def Keplerian_propagation(E0, central_mu, initialDate, finalDate, inertialFrame, nbr_pts):
    
    '''
    ARGS :
    E0 : Initial Vector [a0,e0,i0,pa0,raan0,M0]
    central_mu : mu of the central body (here the earth)
    initialDate : AbsoluteDate of the initial time
    finalDate : AbsoluteDate of the final time when the propagation must stop
    inertialFrame : Inertial Frame of reference used in the construction of orbits and propagation
    nbr_pts : Number of points for the propagation
    '''
    
    # Keplerian parameters
    prop_a,prop_e,prop_i,prop_pa,prop_raan,prop_M,prop_orbits, prop_LM = [],[],[],[],[],[],[],[]
    # Equinoctial parameters :
    prop_Hx, prop_Hy, prop_Ex, prop_Ey = [],[],[],[]
    
    step = finalDate.durationFrom(initialDate)/nbr_pts
    
    a0,e0,i0,pa0,raan0,M0 = E0[0],E0[1],E0[2],E0[3],E0[4],E0[5]
    extrapDate=initialDate
    orbit0 = KeplerianOrbit(float(a0), float(e0) , float(i0), float(pa0), float(raan0), float(M0), PositionAngle.MEAN, inertialFrame, extrapDate, central_mu)

    propagator = KeplerianPropagator(orbit0)

    while (extrapDate.compareTo(finalDate) <= 0.0):
        
        orbit = propagator.propagate(extrapDate, extrapDate.shiftedBy(float(step))).getOrbit()
        PV = orbit.getPVCoordinates()
        keplerian = KeplerianOrbit(PV,inertialFrame,extrapDate,central_mu)
        
        prop_a.append(keplerian.getA())
        prop_e.append(keplerian.getE())
        prop_i.append(keplerian.getI())
        prop_Hx.append(keplerian.getHx())
        prop_Hy.append(keplerian.getHy())
        prop_Ex.append(keplerian.getEquinoctialEx())
        prop_Ey.append(keplerian.getEquinoctialEy())
        prop_LM.append(keplerian.getLM())
        
        ##### RAAN and PA calculations and normalization from Equinoctial parameters
        to_check_raan = float(np.arctan2(prop_Hy[-1],prop_Hx[-1]))
        moduled_raan = to_check_raan % float(mytwopi)
        prop_raan.append(moduled_raan)
       
        # Now we have raan, we also know that ex = e * cos(raan + pa) so pa = arccos(ex/e) - raan
        
        to_check_pa = float(np.arctan2(prop_Ey[-1],prop_Ex[-1])-prop_raan[-1])
        moduled_pa = to_check_pa % float(mytwopi)
        prop_pa.append(moduled_pa)
            
        prop_M.append((prop_LM[-1] - prop_raan[-1] - prop_pa[-1]) % (2*np.pi))

        props_orbits.append(KeplerianOrbit(prop_a[-1],prop_e[-1],prop_i[-1],prop_pa[-1],prop_raan[-1],prop_M[-1], PositionAngle.MEAN, inertialFrame, extrapDate, mu))

        extrapDate = extrapDate.shiftedBy(float(step))

    return prop_a,prop_e,prop_i,prop_pa,prop_raan,prop_M,prop_orbits

I entered the following parameters in input :
E0 = [ 7714425.10389488 , 0.00074884, 1.15259588, 4.64377019, 3.14044603, 1.66140363]
mu = 398600441800000.0 km^3/s².
initialDate = <AbsoluteDate: 1992-10-04T02:26:25.28592Z>
finalDate = <AbsoluteDate: 2004-12-30T10:05:34.201536Z>
inertialFrame = <FactoryManagedFrame: EME2000>
nbr_pts = 8621

The propagation is done for the satellite Topex.
The aim of this propagation is to obtain the keplerian parameters through time. Here is what I got as an example (as expected for the semi-major axis) :

(In red the keplerian propagation in blue the original data from a TLE)
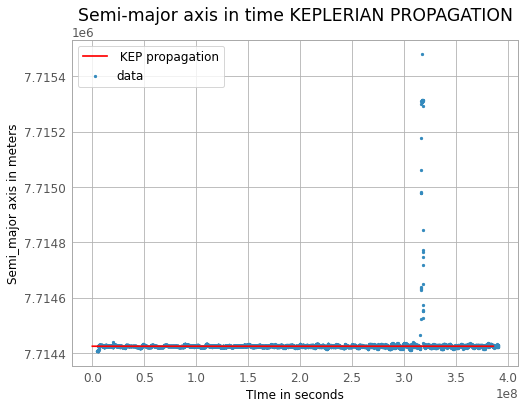
image

But, here is where it’s problematic, all keplerian parameters are correct except the mean anomaly :
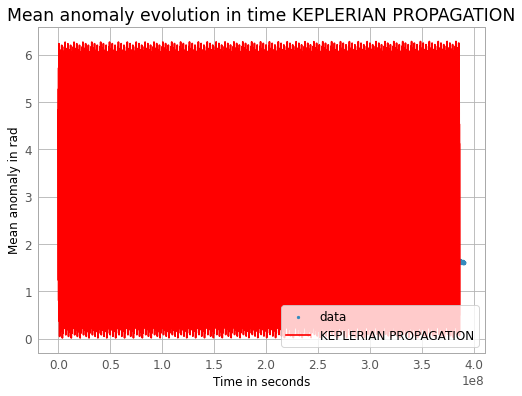
image

While the data (from TLE) look like that :
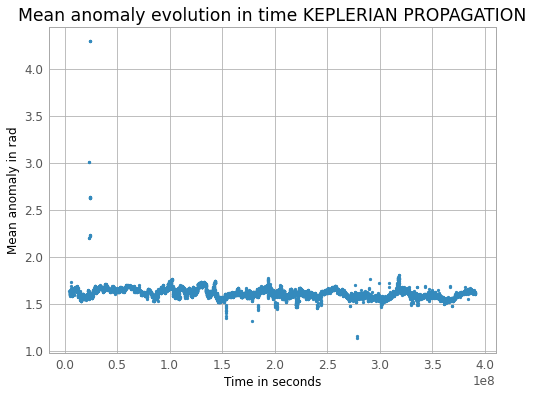
image

I don’t understand what I did wrong here, while all the others parameters seems fine.

Thank you in advance

Julien L.

2

Hi @JulienL,

If your TLE data was retrieved from the SpaceTrack site, I don’t think you’re doing anything wrong. The last graph with the anomaly extracted from the TLE data simply illustrates the fact that TLEs are often generated at dates systematically close to the ascending node as reported on https://celestrak.org/columns/v04n03/ (“Since many element sets are generated with epochs that place the satellite near its ascending node…”). In the case of Topex this translates into an almost constant mean anomaly at these dates.

You can check that the Topex mean anomaly is not constantly fixed by propagating one of the recovered TLEs over a few orbital periods and displaying the orbital parameters at a fixed step of a few minutes.

1 Like
3

Thank you ! In fact I have using SpaceTrack, so it does anwser my question. It was just a matter of periodical extracted data.

Thank you again for your quick answer !