Lunar orbit mean elements

Orekit usage
1

Hello everyone,
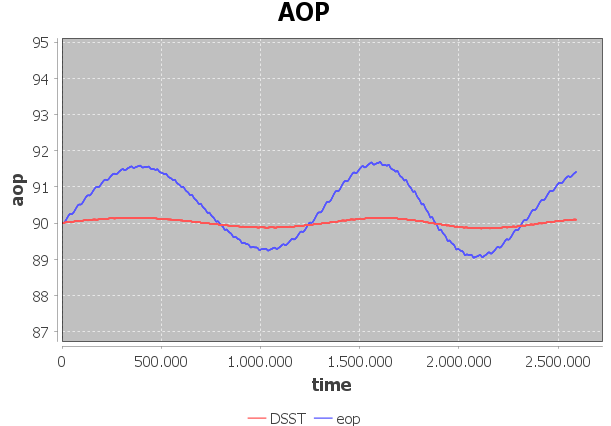
I am working on some Elliptical Lunar Frozen Orbits for my Master’s thesis. I would like to ask if you have any suggestions on how to compute the mean elements of a lunar orbit considering the third-body effect of the Earth, or if you could recommend any papers related to this topic.
I am currently using DSSTPropagator. However, the initial state of the mean elements coincides with the initial state of the osculating elements obtained with NumericalPropagator.
Screenshot 2024-04-26 104332

Orbit keplerianOrbit = new KeplerianOrbit(6142.491723922354e3, 0.6279986005774667, Math.toRadians(56.361858), Math.toRadians(88.32361852647183), Math.toRadians(309.63628514064675), Math.toRadians(258.4590732752806),
        PositionAngleType.TRUE, ReferenceFrame, initialDate, moon_MU); 

  SpacecraftState initialState = new SpacecraftState(keplerianOrbit);

 final double minStepDSST = initialState.getKeplerianPeriod();
               final double maxStepDSST = 10000;
               final double[][] tol = DSSTPropagator.tolerances(10, initialState.getOrbit());
               final DormandPrince54Integrator integratorDSST = new DormandPrince54Integrator(minStepDSST, maxStepDSST, tol[0], tol[1]);
               
               final DSSTPropagator dsstProp = new DSSTPropagator(integratorDSST, PropagationType.MEAN);

 DSSTForceModel earth= new DSSTThirdBody(CelestialBodyFactory.getEarth(), earth_MU);

dsstProp.addForceModel(earth);
                dsstProp.setInitialState(initialState, PropagationType.OSCULATING);

for (int i=0; i<proptime; i+=500)
              {
                double time=i;
                SpacecraftState finalStateDSST= dsstProp.propagate(initialDate.shiftedBy(time));
}

Thank you in advance,
Luna

2

Hi @Luna,

Welcome to Orekit’s forum!

Here the “µ” must be the gravitational parameter of the Moon, it’s a bit counter-intuitive but it’s documented in the Javadoc (see here)

Looking at the code, this is expected. If the propagation has a 0-second duration then the propagator simply returns the initial state, unchanged (this happens here in method AbstractIntegratedPropagator.integrateDynamics). In your case, since the initial state is osculating it returns the osculating state.
It’s a bug or at least a nice-to-have enhancement in my opinion, could you open an issue on the forge please?
In the meantime, to mitigate the problem you can first convert your osculating state to a mean state (before initializing the propagator with it) using DSSTPropagator.computeMeanState.

I would give it a try with Orekit DSST implementation (comparing mean DSST with an osculating numerical propagator on a very high number of orbits) but I’m afraid it won’t work well.
Earth as a third body on lunar orbits is massive and tides effects are not in Orekit’s DSST, plus there are potential resonances that are not taken care of since we mainly use DSST for Earth orbits.
I think DSST should work for, say, a Martian orbit but, unfortunately, the dynamics around the Moon are strongly perturbed by the Earth and the theory must be adapted consequently.

I’ve found two references for semi-analytical satellite theory for a Lunar orbit:

Good luck with your master thesis!

Cheers,
Maxime

1 Like
3

Thank you Maxime for your help.

Kind regards,
Luna