Kalman filter error growth

Orekit usage
1

Hello,

I have been doing some OD using a Kalman filter on data generated using the Generator methods to produce range data with a sigma value of 0.5m. I perform a batch least-squares procedure initially to get a covariance matrix to use with the EKF and I then feed each synthetic measurement into the EKF for processing. I am using the orbit from the generator step as an “exact” solution such that I can determine the error of my OD process in the across-, normal- and along-track directions.

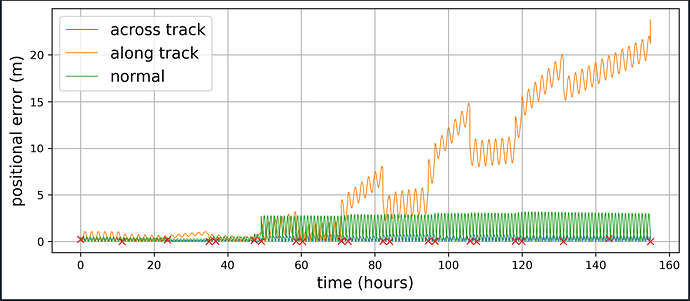
image
image1161×508 126 KB

The figure above shows the results that I get where the red crosses indicate an EKF cycle. Everything is great for the first ~50 hours and the error is kept very low (perhaps unrealistically so as I am not using an atmospheric model yet). In any case, at ~50 hours a sample provided to the EKF causes a “large” jump up in error, particularly in the normal-track direction. Over time this error then leads to more error growth in the along-track direction.

I have two questions about this behavior that I was hoping someone could help with.

  1. Is it expected that a sample in the EKF process can actually cause the estimated state to get worse (I have used a dynamic outlier filter set at 2 sigma) and is there anything that I can do to help it?
  2. It seems that the EKF is unable to recover after this point - is there a reason for the additional measurements not helping get the error back down to the < 5m range? I suspect that it could be the value of Q that I am using for the process noise covariance matrix but am not sure how to better define this object - any references or examples would be appreciated!

My code is below:

    # extract only the satellites we want from the passes list.
    estimator_convergence_thres = conf["propagator_params"]["estimator_convergence_thres"]
    estimator_max_iterations = conf["propagator_params"]["estimator_max_iterations"]
    estimator_max_evaluations = conf["propagator_params"]["estimator_max_evaluations"]
    propagator_tolerance = conf["propagator_params"]["prop_position_error"]
    
    # first we need to use BLS to get an initial covariance matrix for the Kalman filter.
    optimizer = SequentialGaussNewtonOptimizer()
    estimator = SequentialBatchLSEstimator(optimizer, prop_builder)
    estimator.setParametersConvergenceThreshold(estimator_convergence_thres)
    estimator.setMaxIterations(estimator_max_iterations)
    estimator.setMaxEvaluations(estimator_max_evaluations)

    initial_passes=6
     
    for pass_indiv in pass_list[:initial_passes]:
        [estimator.addMeasurement(r) for r in pass_indiv['range']]

    # Perform BatchLSE to obtain the orbital parameters.
    estimated_propagator = estimator.estimate()[0]
    rms = estimator.getOptimum().getRMS()        
    initial_cov = estimator.getPhysicalCovariances(1e-10) # Get covariance at end of initial OD process.
    print(f"\tRMS value of measured-estimated residuals is {rms:.2f} m.")
    
    # now we set up for using a kalman filter.
    initial_guess = estimated_propagator.propagate(estimated_propagator.getInitialState().getDate()).getOrbit()    # initial guess at time
    prop_kalman, prop_builder_kalman, prop_kalman_lvlh = create_orbital_propagator(conf, initial_guess)
    
    # configure an outliers filter for the Kalman filtering process.
    steps_initial_without_filter = 100
    max_sigma = 2.0
    outlier_filter = DynamicOutlierFilter(steps_initial_without_filter, max_sigma)
    
    Q = MatrixUtils.createRealDiagonalMatrix([1e-7, 1e-7, 1e-7, 1e-10, 1e-10, 1e-10])
    
    # Build a Kalman filter.
    kalman = KalmanEstimatorBuilder().addPropagationConfiguration(prop_builder_kalman,
                ConstantProcessNoise(initial_cov, Q)).build()

Thanks so much!
/Paul

2

Hi @Paul1

You are struggling with the dark side of the Kalman filtering :scream:

A Kalman filter somehow interpolates between a state it predicts from previous values and a state that attempts to come closer to measurements as they arrive. If the process noise matrix is high and measurement noise is low, the filter considers its prediction is unreliable but the measurements are good, so it tries hard to follow measurements. If the process noise matrix is low and measurement noise is high, the filter considers its prediction is reliable and measurements are not, so it mostly ignore them as they arrive and uses prediction-only. Tuning the covariance matrices (both process and measurement) is akin to black magic in my humble opinion. Failing to do it properly may imply divergence. I think this is what you observe. At some point the balance between trusting the prediction and trusting the measurement leads to a slightly wrong state. Then the following measurements are probably disregarded because they are too far from the predicted state: the filter considers the measurements are wrong when in fact it is the predicted state that is wrong. Starting from this, all subsequent measurements will be rejected, the filter has diverged.

1 Like
3

Hi @Paul1,

Looking at your figure, it is indeed weird that your estimation is getting that worse at 50 hours with the Kalman filter, especially when using simulated measurements with a “perfect” Gaussian noise. Have you checked the measurements at that point ?

It can happen yes. I guess you’re using the same model (i.e. propagator) for measurements’ simulation and Kalman OD ? In that case what you see is purely the error introduced in the measurements.
However I find it weird that the normal error jumps like this at 50 hours.

As Luc said, Kalman filters are hard to tune, especially the process noise matrix Q.
Looking at the drift on the along-track component it seems that the Kalman gain is too small to correct the orbit, so it’s possible that the covariance matrix gets too small. But with a filter at 2σ the measurements should be rejected with such an error, so I’m not sure.
We do have an example in the tutorials, maybe this will help you: KalmanNumericalOrbitDetermination.

This is what I would suggest for going further:

  1. Plot the covariances, at least the diagonal values, it will really help you understand what happens within the filter.
  2. Use a KalmanObserver (example in the tutorial here) to log each measurement and its innovation, correction, the covariance of the filter etc. Again it will help you understand what happens, especially around 50 hours.
  3. Start with a very simple test (with a process noise at 0 for example, and/or a very low measurement noise and no outlier filter) and progressively incorporate more complexity.

I hope this will help you,
Maxime

1 Like