Hello everyone!!
I’ve been trying to implement IodGooding (specifically Orbit got from three angular observations!!) recently, but I’ve got super unsuccessful result for it.
I used real observations of GSS:
LAT = 43.05722 # North
LON = 76.971667 # West
ALT = 2735.0 # meters
t1 = Time('2023-06-09T17:04:59.10', format='isot', scale='utc')
t2 = Time('2023-06-09T17:10:50.66', format='isot', scale='utc')
t3 = Time('2023-06-09T17:16:21.09', format='isot', scale='utc')
RA = np.array([(15*(16+5/60+51.20/3600)),
(15*(16+11/60+43.73/3600)),
(15*(16+17/60+15.1/3600))])
DEC = np.array([(-(6+31/60+44.22/3600)),
(-(6+31/60+52.36/3600)),
(-(6+32/60+0.03/3600))])
or data with a time days apart, thus nRev is more than 0 (let’s consider it as 2nd case):
t1 = Time('2019-06-22T15:57:15.87', format='isot', scale='utc')
t2 = Time('2019-06-23T15:57:16.87', format='isot', scale='utc')
t3 = Time('2019-06-24T17:01:04.87', format='isot', scale='utc')
RA = np.array([(15*(15+54/60+36.81/3600)),
(15*(15+58/60+33.43/3600)),
(15*(17+0/60+59.51/3600))])
DEC = np.array([(-(6+2/60+0.16/3600)),
(-(6+1/60+59.38/3600)),
(-(6+32/60+53.21/3600))])
For calculating position I used IOD with Gauss Method.ipynb.
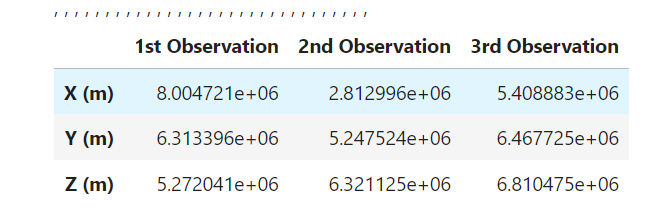
r1_vec = position[0]
r2_vec = position[1]
r3_vec = position[2]
r1=(np.dot(r1_vec,r1_vec))**0.5
r2=(np.dot(r2_vec,r2_vec))**0.5
r3=(np.dot(r3_vec,r3_vec))**0.5
# Initialization of Gooding IOD Method
gooding = IodGooding(Mu)
ITRF = FramesFactory.getITRF(IERSConventions.IERS_2010, True) # Define ECEF reference frame.
earth = OneAxisEllipsoid(Re, f, ITRF)
# Frame of the ground station is given as Topocentric Frame.
station_coord = GeodeticPoint(LAT, LON, ALT)
station_frame = TopocentricFrame(earth, station_coord, "N42")
# Create the ground station.
ground_station = GroundStation(station_frame)
# Create the observable satellite object, name it 1 as default
obs_sat = ObservableSatellite(1)
sigma = [1.0, 1.0]
baseW = [1.0, 1.0]
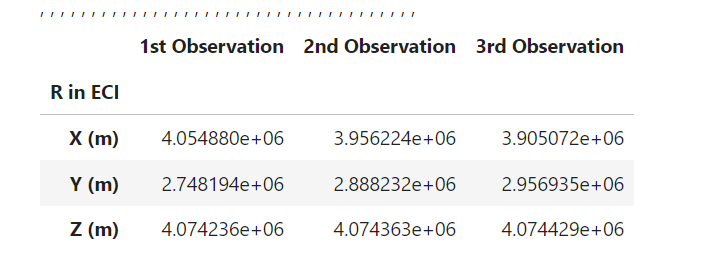
raDec1 = AngularRaDec(ground_station, FramesFactory.getEME2000(), datetime_to_absolutedate(t1.datetime),
[float(np.radians(RA[0])), float(np.radians(DEC[0]))], sigma, baseW, obs_sat)
raDec2 = AngularRaDec(ground_station, FramesFactory.getEME2000(), datetime_to_absolutedate(t2.datetime),
[float(np.radians(RA[1])), float(np.radians(DEC[1]))], sigma, baseW, obs_sat)
raDec3 = AngularRaDec(ground_station, FramesFactory.getEME2000(), datetime_to_absolutedate(t3.datetime),
[float(np.radians(RA[2])), float(np.radians(DEC[2]))], sigma, baseW, obs_sat)
nRev = int(t3.jd - t1.jd)
estimated_orbit_Gooding = gooding.estimate(ECI, raDec1, raDec2, raDec3, float(r1), float(r3), nRev, True)
In 1st case I’ve got next result:
GIBBS Kepler elements:
Keplerian parameters: {a: 4.240057888814118E7; e: 0.004565616165528337; i: 0.09156350509937108; pa: 169.65363782985855; raan: 91.0134171094278; v: -18.903633576322076;}
GOODING Kepler elements:
Keplerian parameters: {a: 6.4562346547382206E7; e: 0.2776002076596247; i: 12.165627396844142; pa: -100.77301045351494; raan: -27.59808364817013; v: 11.47979431436121;}
It’s clear, that somethings works not so well with IodGooding. Then I thought that the reason may hide in input data itself. So i tried to run the 2nd case, but it didn’t work, giving out NaN for every element.
I’ll be glad for every thought, that you may have on reason of that strange behavior of IodGooding. Thank you in advance!!