Hello Everyone,
I’ve found some strange behavior. The batch least squares is not converging in a I would expect. First let me describe my methodology. I first take an orbit (I’ll refer to this as the true orbit) and propagate it forward. I have a groundstation mimicking a radar. When the true orbit encounters the edge of the radar, the propagation stops takes angular and range observations and propagates forward ten seconds, stops, and takes another set of observations until the true orbit exits the field of view of the groundstation. I then take the first, middle and last observations to produce an orbital estimate using herrick gibbs. I then use a LevenbergMarquardt least squares optimizer to run batch least squares with the herrick gibbs guess as an initial guess and all the observations as input. My comparisons from the BLS converged orbit and the true orbit is done using Mahalanobis Distance (Basically standard deviation distance).
Well I’ve found some strange behavior. First using perfect, no error observations does not cause the BLS to converge on the correct answer, even if I use the truth as oppose to the herrick gibbs as the input. That is strange issue number one.
Secondly, the more observations I feed into the least squares, the greater the number of deviations the converged orbit is from the true orbit. This is counter intuitive.
Finally the last if I take the covariance and propagate it forward, and compare it to the true orbit once again, a weird amplifying sinusoidal error. Check it out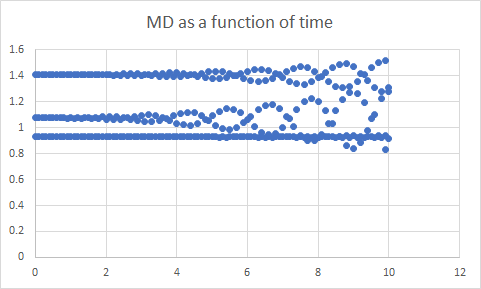
The x axis is days and y axis mahalanobis distance (lower is better). The lowest line is 14 observations, the one above 15 and the highest is 19 observations. This graph was done using perfect no error observations.
Now from looking at the covariance matrices, it looks as if they are somewhat close to being singular, and also the main contribution seem to come from the eccentricity and semimajor axis error. In fact from the covariance matrix it seems they are highly correlated (0.9+)
I believe these errors are probably all stemming from the same issue. They are present when using all orbital elements, but seem to be worse in keplarian than equinoctial, and worst in Cartesian. My only theory is that the problem is from numerical inaccuracies stemming from the starting and stopping of the propagation of the true orbit.
Does anyone have any suggestions or input?