FieldNumericalPropagator doesn't reproduce same results as normal propagator at the reference

Orekit MATLAB usage
1

Hello, I’m new to the forum and wanted to post about some weird behaviour that I am experimenting with the FieldNumericalPropagator. My goal was to compare the differences in precision between different taylor order aproximations for a propagation (w.r.t a normal propagation, NumericalPropagator, under the same configuration), but was surprised to see that even the reference of the taylor prop. doesn’t map to the same result as the normal propagator, with the difference being in the order of 0.3 mm (position error) after 3 days. I know it isn’t a lot but I expected the same result up to numerical precision so I am a bit confused. Where does the difference comes from? Isn’t the taylor propagator doing the same as the normal one with the real part of the input?

All aspects of the propagation are the same: same initial conditions, dynamical model (all perturbations are the same), and tolerances.

I can post all scripts in case someone wants to check, but for now I will post only the function that is used to create the propagator object, as I think that should suffice to know if I am doing something wrong in the configuration for each case (taylor_order>=0 makes the configuration to use the FieldNumericalPropagation).

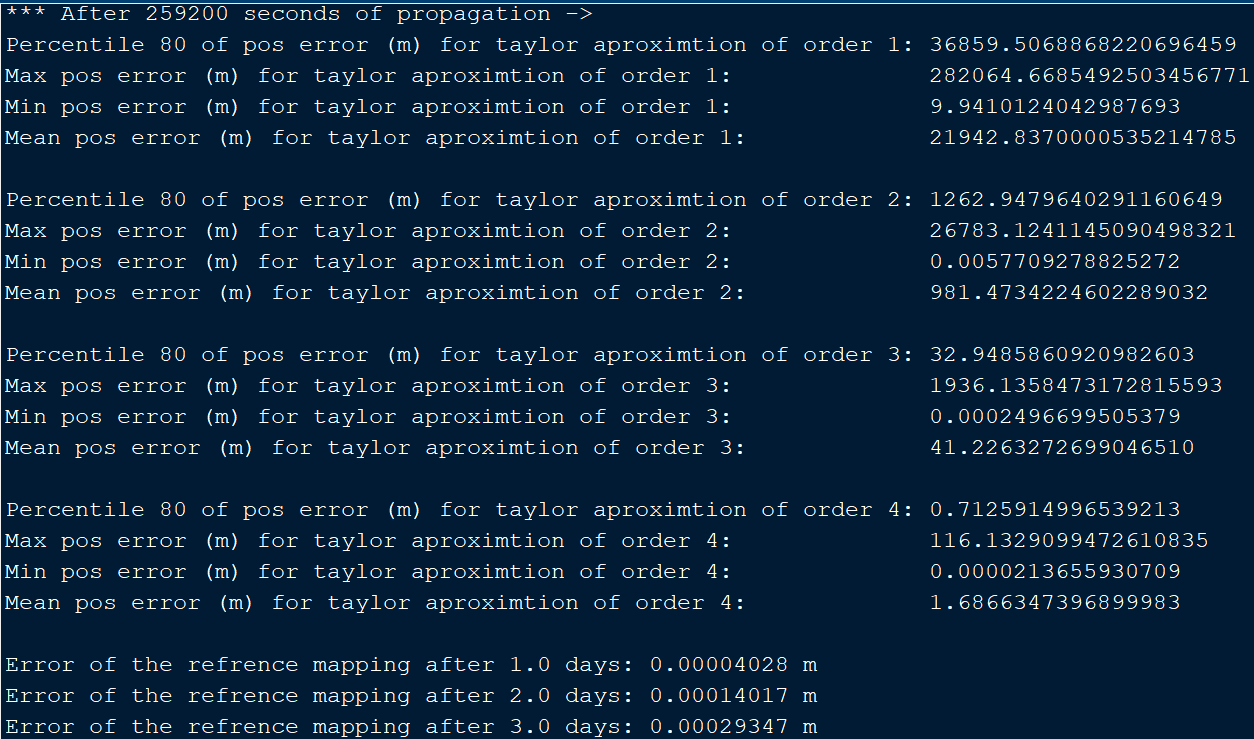
Here I leave as well a screenshot of the error statistics for the cloud of points that I am using to compare, and the error of the reference mapping as well:

taylor
taylor1254×739 41.6 KB

Thanks in advance for any tip that could help me understand this discrepancies.

createPropagator.m (9.1 KB)

2

At this level of precision, I would say the discrepancy cannot be avoided.
The Field propagation performs the same operations as the double propagation, but these operations may be reorganized by the compiler. Even a simple operation like a x + b y + c z could be performed differently depending on compiler internal choices (which operation to perform first, keep the intermediate results in registers or store them in memory, type of the processor and number of guard bits…). We try to reduces this effects to a maximum (hence using methods like MathArrays.linearCombination for the expression above instead of the naive implementation), but we will never completely suppress this.
I guess what you observe is simply the result of numerical noise that occurs at some point on the last bit or so and that increases progressively as time flows. In fact, as you use drag force which is really highly dependent on position, I am even surprised you get only 0.3mm after 3 days; this seems already pretty stable to me.

3

Thanks @luc, that seems totally reasonable to me. I guessed that it had something to do with numerical precision but I’m not any kind of expert on how these things work internally. With this in mind I think I can use the taylor propagator without worries.

Again, many thanks!