Hello! It’s me again 
Here is the code that I ended up using to compute ERP using the CERES SYN1DEG data. It does not (although it should for real geodetic grade POD) include angular distribution models based on the land surface type and cloud types (outlined here if anyone is ever interested).
Sorry it is a bit “hacky” in some places and I use a number of my own helper functions- I imagine some of these already exist in orekit, but it was just faster for me to use these 
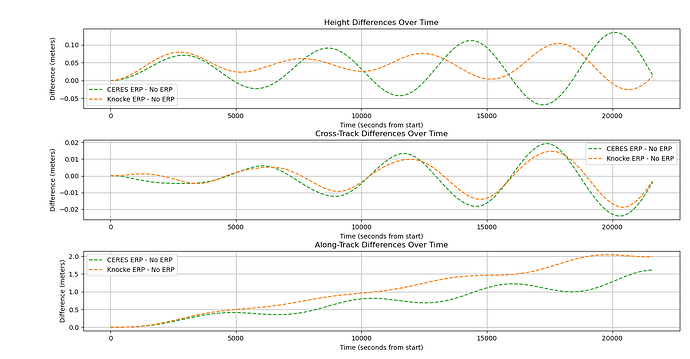
I took a starlink TLE as initial conditions and propagated for 6 hours
- Once with just 10,10 gravity field
- Once with 10,10 gravity field and
KnockeRediffusedForceModel
- Once with 10,10 gravity field and the method below.
both methods are quite similar.
I would love to hear if anyone had any suggestions for improvements.
Thanks again for your help @Vincent !!
import orekit
from orekit.pyhelpers import setup_orekit_curdir, absolutedate_to_datetime
orekit.pyhelpers.download_orekit_data_curdir()
vm = orekit.initVM()
setup_orekit_curdir()
from org.orekit.utils import Constants, PVCoordinates, IERSConventions
from org.orekit.forces import PythonForceModel
from org.orekit.frames import FramesFactory
from org.orekit.bodies import OneAxisEllipsoid
from org.hipparchus.geometry.euclidean.threed import Vector3D
from orekit import JArray_double
from java.util import Collections
from java.util.stream import Stream
from tools.utilities import find_nearest_index, lla_to_ecef, julian_day_to_ceres_time
from tools.data_processing import calculate_satellite_fov, is_within_fov_vectorized, sat_normal_surface_angle_vectorized
import numpy as np
def compute_erp_at_sc(ceres_time_index, radiation_data, sat_lat, sat_lon, sat_alt, horizon_dist):
# Earth radius in meters
R = Constants.WGS84_EARTH_EQUATORIAL_RADIUS
# Latitude and longitude arrays
lat = np.arange(-89.5, 90.5, 1) # 1-degree step from -89.5 to 89.5
lon = np.arange(-179.5, 180.5, 1) # 1-degree step from -179.5 to 179.5
# Mesh grid creation
lon2d, lat2d = np.meshgrid(lon, lat)
# FOV calculations
fov_mask = is_within_fov_vectorized(sat_lat, sat_lon, horizon_dist, lat2d, lon2d)
radiation_data_fov = np.ma.masked_where(~fov_mask, radiation_data[ceres_time_index, :, :])
cos_thetas = sat_normal_surface_angle_vectorized(sat_alt, sat_lat, sat_lon, lat2d[fov_mask], lon2d[fov_mask])
cosine_factors_2d = np.zeros_like(radiation_data_fov)
cosine_factors_2d[fov_mask] = cos_thetas
# Adjusting radiation data
adjusted_radiation_data = radiation_data_fov * cosine_factors_2d
# Satellite position and distance calculations
sat_ecef = np.array(lla_to_ecef(sat_lat, sat_lon, sat_alt))
ecef_x, ecef_y, ecef_z = lla_to_ecef(lat2d, lon2d, np.zeros_like(lat2d))
ecef_pixels = np.stack((ecef_x, ecef_y, ecef_z), axis=-1)
vector_diff = sat_ecef.reshape((1, 1, 3)) - ecef_pixels
distances = np.linalg.norm(vector_diff, axis=2) * 1000 # Convert to meters
# Radiation calculation
delta_lat = np.abs(lat[1] - lat[0])
delta_lon = np.abs(lon[1] - lon[0])
area_pixel = R**2 * np.radians(delta_lat) * np.radians(delta_lon) * np.cos(np.radians(lat2d)) # Convert to m^2
P_rad = adjusted_radiation_data * area_pixel / (np.pi * distances**2) # map of power flux in W/m^2 for each pixel
#need to convert the vector_diff to eci frame
unit_vectors = vector_diff / distances[..., np.newaxis] * 1000 # Convert to unit vectors in meters
radiation_force_vectors = unit_vectors * P_rad[..., np.newaxis] / (299792458) # Convert to Newtons
# Summing all force vectors
total_radiation_force_vector = np.sum(radiation_force_vectors[fov_mask], axis=0)
# Satellite area in square meters
satellite_area = 10.0
# Total force due to radiation pressure (not including reflection for now)
total_force = total_radiation_force_vector * satellite_area
# Satellite mass in kilograms
satellite_mass = 500.0
# Calculate acceleration
acceleration_vector = total_force / satellite_mass
scalar_acc = np.linalg.norm(acceleration_vector)
print(f"scalar_acc:{scalar_acc}m/s^2")
down_vector = - sat_ecef / np.linalg.norm(sat_ecef) # Normalize the satellite's position vector to get the down vector
total_radiation_vector_normalized = total_radiation_force_vector / np.linalg.norm(total_radiation_force_vector) # Normalize the total radiation vector
cos_theta = np.dot(total_radiation_vector_normalized, down_vector) # Cosine of the angle
angle_radians = np.arccos(cos_theta) # Angle in radians
angle_degrees = np.rad2deg(angle_radians) # Convert to degrees
return np.array(acceleration_vector), scalar_acc, angle_degrees
class CERES_ERP_ForceModel(PythonForceModel):
def __init__(self, ceres_times, combined_radiation_data):
super().__init__()
self.scalar_acc_data = []
self.erp_angle_data = []
self.time_data = []
self.ceres_times = ceres_times
self.combined_radiation_data = combined_radiation_data
def acceleration(self, spacecraftState, doubleArray):
# Compute the current altitude within the acceleration method
pos = spacecraftState.getPVCoordinates().getPosition()
alt_m = pos.getNorm() - Constants.WGS84_EARTH_EQUATORIAL_RADIUS
alt_km = alt_m / 1000.0
horizon_dist = calculate_satellite_fov(alt_km)
# Get the AbsoluteDate
absolute_date = spacecraftState.getDate()
# Convert AbsoluteDate to Python datetime
date_time = absolutedate_to_datetime(absolute_date)
# convert date_time to julianday
jd_time = date_time.toordinal() + 1721425.5 + date_time.hour / 24 + date_time.minute / (24 * 60) + date_time.second / (24 * 60 * 60)
# Get the ECI and ECEF frames
ecef = FramesFactory.getITRF(IERSConventions.IERS_2010, True)
# Transform the position vector to the ECEF frame
pv_ecef = spacecraftState.getPVCoordinates(ecef).getPosition()
# Define the Earth model
earth = OneAxisEllipsoid(
Constants.WGS84_EARTH_EQUATORIAL_RADIUS,
Constants.WGS84_EARTH_FLATTENING,
ecef)
# Convert ECEF coordinates to geodetic latitude, longitude, and altitude
geo_point = earth.transform(pv_ecef, ecef, spacecraftState.getDate())
# Extract latitude and longitude in radians
latitude = geo_point.getLatitude()
longitude = geo_point.getLongitude()
# Convert radians to degrees if needed
latitude_deg = np.rad2deg(latitude)
longitude_deg = np.rad2deg(longitude)
ceres_time = julian_day_to_ceres_time(jd_time)
ceres_indices = find_nearest_index(self.ceres_times, ceres_time)
erp_vec, scalar_acc, erp_angle = compute_erp_at_sc(ceres_indices, self.combined_radiation_data, latitude_deg, longitude_deg, alt_km, horizon_dist)
# convert the erp_vec to ECI
eci = FramesFactory.getEME2000()
# Transform the position vector to the ECI frame
transform = ecef.getTransformTo(eci, spacecraftState.getDate())
erp_vec_ecef_pv = PVCoordinates(Vector3D(float(erp_vec[0]), float(erp_vec[1]), float(erp_vec[2])))
# Transform the ERP vector to ECI frame
erp_vec_eci_pv = transform.transformPVCoordinates(erp_vec_ecef_pv)
# Extract the transformed vector components
erp_vec_eci = erp_vec_eci_pv.getPosition()
# Store the scalar acceleration and other data
self.scalar_acc_data.append(scalar_acc)
self.erp_angle_data.append(erp_angle)
self.time_data.append(jd_time)
# Create the Orekit vector for the ERP force in ECI frame
orekit_erp_vec = Vector3D(erp_vec_eci.getX(), erp_vec_eci.getY(), erp_vec_eci.getZ())
# print("orekit_erp_vec components:", orekit_erp_vec.getX(), orekit_erp_vec.getY(), orekit_erp_vec.getZ())
return orekit_erp_vec
def addContribution(self, spacecraftState, timeDerivativesEquations):
timeDerivativesEquations.addNonKeplerianAcceleration(self.acceleration(spacecraftState, None))
def getParametersDrivers(self):
return Collections.emptyList()
def init(self, spacecraftState, absoluteDate):
pass
def getEventDetectors(self):
return Stream.empty()