Accuracy with initial state and setup of DSST and numerical propagator

[Eirik]

Hello Orekit community!

I’m using the Orekit python wrapper to calculate reentry estimates for several smaller satellites in LEO. They are distributed from 550km to 620km altitude in SSO orbits. I’ve been using numerical and DSST propagator, and experimented with integrators and other settings. I’ve got a few questions that I was hoping someone could help to answer!

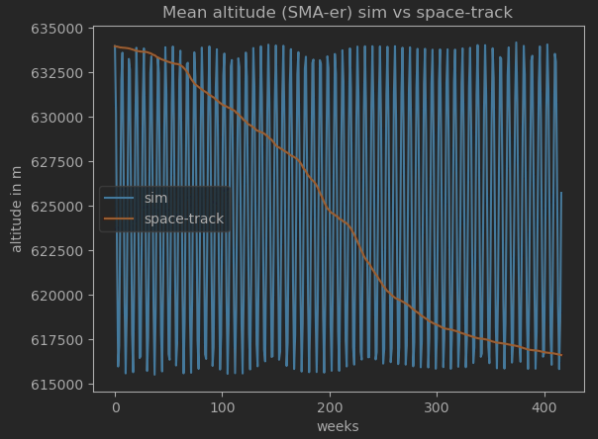
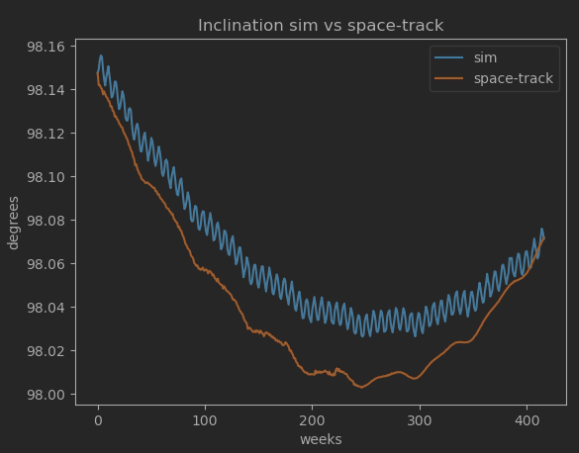
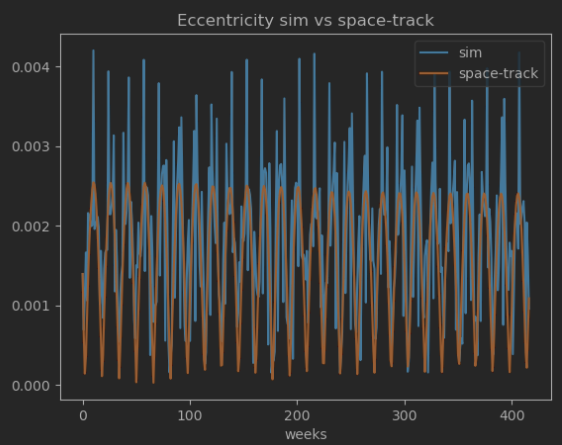
Since one main uncertainty comes from the drag force, my plan is to compare an OREKit propagation to historical data, and use this to estimate the drag coefficient before I propagate to reentry. I have most of the other properties for the satellite: mass, surface area, attitude, etc. When I have estimated a drag coefficient, I think the main uncertainty for the reentry should be atmospheric variation predictions. But when I adjust the drag coefficient so that the orbit altitude match the historical data, other parameters like inclination, eccentricity and beta angle are still slightly off…

I suppose the initial state is a source of such errors. I’m currently gathering TLEs from Space-track to use for initial state. First I simply used the TLE propagator to create a spacecraft state and then convert it to a Keplerian orbit and use this for creating an initial state. Is this a good approach?

I then got the advice to convert the TLE to a propagator using “FiniteDifferencePropagatorConverter”. The problem is that I see very different results when I adjust the integrator and converter settings. Could anyone recommend an integrator and reasonable step sizes, and threshold + duration for conversion?

I also tried to use several states from several TLEs as input to the conversion. Shouldn’t this approach be possible to use to gain higher accuracy? In my simulation the result was worse than with a single state.

As I mentioned I have used both the numerical propagator and the DSST propagator. With the DSST I get a smooth output, but with the numerical propagator the orbit altitude swings up and down around 15 km with a period of a couple of months. Is this expected behavior, or am I doing something wrong?

Thanks in advance!
Eirik

#Setting up integrator and DSST propagator and implementing forces
dsst_integrator = ClassicalRungeKuttaIntegrator(startTLEState.getKeplerianPeriod()*5)
dsstProp = DSSTPropagator(dsst_integrator)

dsstProp.setInitialState(startTLEState, PropagationType.MEAN)
dsstProp.addForceModel(DSSTTesseral(earth.getBodyFrame(),7.292115E-5, harmonicsProvider))
dsstProp.addForceModel(DSSTZonal(harmonicsProvider))
dsstProp.addForceModel(DSSTAtmosphericDrag(spacecraftDrag,mu))
dsstProp.addForceModel(DSSTThirdBody(sun,mu))
dsstProp.addForceModel(DSSTThirdBody(moon,mu))
dsstProp.addForceModel(DSSTSolarRadiationPressure(sun,Constants.EIGEN5C_EARTH_EQUATORIAL_RADIUS,IsotropicRadiationSingleCoefficient(sat_cross_section, sunRad_coef),mu))

#Setting up numerical propagator and implementing forces
minStep = 1e-3
maxStep = 500.0
tol = NumericalPropagator.tolerances(0.001, startTLEState.getOrbit(), OrbitType.KEPLERIAN)

num_integrator = DormandPrince853Integrator(minStep, maxStep,
    JArray_double.cast_(tol[0]),  # Double array of doubles needs to be cast in Python
    JArray_double.cast_(tol[1]))
num_integrator.setInitialStepSize(60.0)

numProp = NumericalPropagator(num_integrator)
numProp.setInitialState(startTLEState)
numProp.addForceModel(attractionModel)
numProp.addForceModel(spacecraftDrag)
numProp.addForceModel(ThirdBodyAttraction(sun))
numProp.addForceModel(ThirdBodyAttraction(moon))
numProp.addForceModel(SolarRadiationPressure(sun,Constants.EIGEN5C_EARTH_EQUATORIAL_RADIUS,IsotropicRadiationSingleCoefficient(sat_cross_section, sunRad_coef)))

[Serrof]

Hello and welcome,

I see at least a couple points of attention here.

You pass the same initial state to both propagators but you define it as a “mean” one for DSST. For consistency, you should probably say it’s osculating. This is the DSST input, you can still define its output to be osculating or mean.

About the tolerances for Dormant Prince, you compute them for Keplerian elements, but you need to know that by default, a NumericalPropagator uses equinoctial ones. I wouldn’t advise to use Keplerian coordinates for propagation so you ought to change your tolerances.

Cheers,
Romain.

[Eirik]

Hi Romain,
Thank you for the reply! I have adjusted the two settings you pointed out. For the numerical propagator, changing from keplerian to equinocial orbit type did not change the output, the graphs of orbit altitude and inclination/eccentricity look pretty much the same as the ones I posted with very oscillating values.

For the DSST propagator, the propagation now stopped after 80 weeks with the error message “OrekitException: unable to compute mean orbit from osculating orbit after 201 iterations”. The output from these first 80 weeks looks very different from the previous output though, with oscillating parameters instead of a smooth graph…

Thanks,
Eirik

[Serrof]

Hi,

I feel like you’ve changed the propagation type output rather than just the one of the input initial orbit. This will give you more accurate results for your post process as it is, but also makes the run more expensive (and prone to errors like the one you get). Try that:

dsstprop = DSSTPropagator(integrator, PropagationType.MEAN)

dsstprop.setInitialState(state, propagatonType.OSCULATING)

However, in Orekit 11, DSST is missing things like the second order J2 term, so it’s probably not well suited for applications like reentry prediction

Romain.