What is the difference between using 64 or 32 for the value of gravity degree and order, and whether the larger the value, the more accurate the orbit estimation. Then can I fix the setting to 64. And I found that using 64 or 32, the results of orbit estimation and the estimated cd are somewhat different.
Thanks!
Hi @newWL
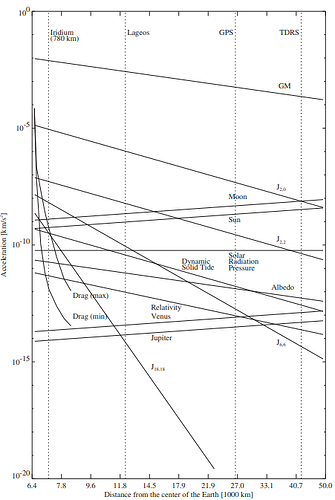
Let me answer your question with the following image from Montenbruck and Gill, Satellite Orbits
It presents the impact of orbital perturbations depending satellite’s altitude.
Best regards,
Bryan
thanks! I’ll study it.
The picture represents the acceleration due to the various perturbations as a function of the distance from the Earth. As expected, the higher the geopotential order considered, the smaller its corresponding acceleration will be. For instance, consider the J(6,6) and J(18,18) terms: over the same altitude range, the first results in accelerations in the range [1e-8, 1e-12] km/s^2, whereas the second in the range [1e-9, 1e-20] km/s^2.
This means that if you consider a geopotential expansion up to 64x64, the additional contributions are even smaller and they drop off even faster with increasing altitude. The degree and order you need in your model are a factor of the altitude of your orbit and of the accuracy you want to achieve.
Another factor that is worth keeping in mind is the uncertainty on your other force models (or their overall presence). It doesn’t make sense to have one perturbation modelled to an incredibly high precision, while others are modelled very poorly, since all the extra computations used to model the gravity field will be wasted. Also, consider the Lageos altitude (the second dotted vertical line): in this case, if your model doesn’t include the third body attraction of Venus and Jupiter, it’s useless to consider a high order gravity model, since you’d be neglecting more relevant accelerations.
Best regards,
Emiliano
Thank you very much, I still do not fully understand your statement. Is there more detailed information on this?